Tìm nghiệm của đa thức \(Q\left( x \right) = 2{x^2} + x\).
Ta có:
\(\begin{array}{l}2{x^2} + x = 0\\x\left( {2x + 1} \right) = 0\end{array}\)
\( \Rightarrow x = 0\) hoặc \(x = - \dfrac{1}{2}\)
Vậy \(Q\left( x \right)\) có nghiệm là \(x = 0;\,x = - \dfrac{1}{2}\).
Tính \(A\left( { - 1} \right);A\left( { - 2} \right).\)
Ta có :
\(\begin{array}{l}A\left( { - 1} \right) = {\left( { - 1} \right)^4} - {\left( { - 1} \right)^2} + 1 = 1\\A\left( { - 2} \right) = \,{\left( { - 2} \right)^4} - {\left( { - 2} \right)^2} + 1 = 13\end{array}\).
Tìm bậc của đa thức trên.
\(A\left( x \right)\) có bậc 4.
Tìm bậc của đa thức trên.
\(A\left( x \right)\) có bậc 4.
Chọn câu đúng.
Ta có: \(\Delta KBC\) cân tại \(K\) (theo câu trước)
\( \Rightarrow BK = CK\)
Ta có: \(BK + CK = BK + BK = 2BK = 2.2KM = 4KM\) (tính chất đường trung tuyến).
Mà \(\Delta KBC\) có: \(KB + KC > BC\) (bất đẳng thức tam giác)
Suy ra: \(BC < 4.KM\)
Tam giác\(\,\Delta BKC\) là tam giác.
Theo câu trước ta có: \(\Delta BNC = \Delta CMB\)
Do \(\Delta BNC = \Delta CMB\)
\( \Rightarrow \widehat {MBC} = \widehat {NCB}\) (hai góc tương ứng)
\( \Rightarrow \Delta KBC\) cân tại \(K.\)
Chọn câu đúng.
Xét \(\Delta BNC\) và \(\Delta CMB\) có:
\(\begin{array}{l}BN = AN = \dfrac{{AB}}{2};\,\\CM = AM = \dfrac{{AC}}{2}\end{array}\)
Mà \(AB = AC\) \( \Rightarrow BN = CM\)
Lại có:
+) \(\widehat B = \widehat C\) (do \(\Delta ABC\) cân tại A)
+) \(BC\) cạnh chung.
Do đó: \(\Delta BNC = \Delta CMB \left( {c.g.c} \right)\).
Chọn câu đúng.
Xét \(\Delta BNC\) và \(\Delta CMB\) có:
\(\begin{array}{l}BN = AN = \dfrac{{AB}}{2};\,\\CM = AM = \dfrac{{AC}}{2}\end{array}\)
Mà \(AB = AC\) \( \Rightarrow BN = CM\)
Lại có:
+) \(\widehat B = \widehat C\) (do \(\Delta ABC\) cân tại A)
+) \(BC\) cạnh chung.
Do đó: \(\Delta BNC = \Delta CMB \left( {c.g.c} \right)\).
Bậc của đa thức \(f\left( x \right) = - 7{x^4} + 4{x^3} + 8{x^2} - 5{x^3} - {x^4} + 5{x^3} + 4{x^4} + 2020\) là:
Ta có:
\(f\left( x \right) = - 7{x^4} + 4{x^3} + 8{x^2} - 5{x^3} - {x^4} + 5{x^3} + 4{x^4} + 2020\)\(= \left( { - 7{x^4} - {x^4} + 4{x^4}} \right) + \left( {4{x^3} - 5{x^3} + 5{x^3}} \right) + 8{x^2} + 2020\)\( = - 4{x^4} + 4{x^3} + 8{x^2} + 2018\)
\( \Rightarrow \) Bậc của đa thức \(f\left( x \right)\) là: \(4.\)
Cho bảng tần số:

Mốt của dấu hiệu là:
Giá trị 30 có tần số lớn nhất là 10.
Suy ra 30 là mốt của dấu hiệu. Hay \({M_0} = 30\).
Nếu \(AM\) là đường trung tuyến và \(G\) là trọng tâm của tam giác \(ABC\) thì:
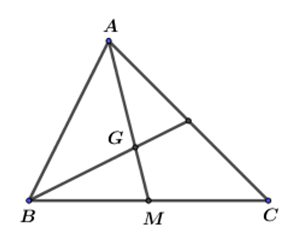
Dựa vào định lý ba đường trung tuyến của tam giác ABC.
Ta có: \(AG = \dfrac{2}{3}AM\).
Độ dài hai cạnh góc vuông liên tiếp lần lượt là \(5cm\) và \(12cm\) thì độ dài cạnh huyền là:
Ta có: \({5^2} + {12^2} = {13^2} \Rightarrow \) cạnh huyền bằng 13cm.
Số nào sau đây là nghiệm của đa thức \(A\left( x \right) = 3x - 2\).
Ta có:
\(\begin{array}{l}A\left( x \right) = 3x - 2 = 0\\ \Leftrightarrow \,3x = 2\\ \Leftrightarrow x = \dfrac{2}{3}\end{array}\).
Đơn thức thích hợp điền vào chỗ trống (…) trong phép toán: \(4{x^3} + ... = - 5{x^3}\) là:
Ta có: \(4{x^2} + ... = - 5{x^3}\)\( \Rightarrow \) Đơn thức cần tìm là: \( - 5{x^3} - 4{x^3} = - 9{x^3}\).
Đơn thức nào sau đây đồng dạng với đơn thức \( - 3x{y^2}\).
Đơn thức khác hệ số và có cùng phần biến với đơn thức \( - 3x{y^2}\) là: \(\left( { - 8xy} \right)y = - 8x{y^2}\).
Kết quả của phép tính \( - 5{x^2}{y^5} - {x^2}{y^5} + 3{x^2}{y^5}\).
Ta có: \( - 5{x^2}{y^5} - {x^2}{y^5} + 3{x^2}{y^5} = \left( { - 5 - 1 + 3} \right){x^2}{y^5} = - 3{x^2}{y^5}\).
Giá trị của biểu thức \(3{x^2}y + 3{x^2}y\) tại \(x = - 2\) và \(y = - 1\) là:
Thu gọn đa thức ta được: \(3{x^2}y + 3{x^2}y = 6{x^2}y\).
Thay \(x = - 2;\,y = - 1\) vào biểu thức đã được thu gọn ta có: \(6.{\left( { - 2} \right)^2}\left( { - 1} \right) = - 24\).
Đa thức \(g\left( x \right) = {x^2} + 2\).
Ta thấy: \(g\left( x \right) = {x^2} + 2\) luôn luôn lớn hơn 0 nên đa thức không có nghiệm.
Tam giác có một góc \({60^0}\) thì với điều kiện nào thì trở thành tam giác đều:
Tam giác có một góc bằng \({60^0}\) và có hai cạnh bằng nhau là tam giác đều.
Cho tam giác \(ABC\) có \(\widehat C = {40^0};\,\widehat B = {60^0}.\) Câu nào sau đây đúng?
Tam giác \(ABC\) có: \(\widehat C = {40^0};\,\widehat B = {60^0}.\)
\( \Rightarrow \) \(\widehat A = {180^0} - \left( {{{40}^0} + {{60}^0}} \right) = {80^0}\)
Trong một tam giác cạnh đối diện với góc lớn hơn thì lớn hơn.
Ta có:
\(\begin{array}{l}\widehat A > \widehat B > \widehat C\,\,\left( {{{80}^0} > {{60}^0} > {{40}^0}} \right)\\ \Rightarrow BC > AC > AB\end{array}\).

