Tứ giác $EIFK$ là hình gì?
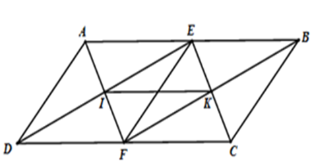
Theo câu trước ta có tứ giác \(BEDF\) là hình bình hành nên \(ED = BF;\,ED//BF \Rightarrow EI//FK\,\left( 1 \right)\)
Theo câu trước ta có tứ giác \(AEDF\) và \(BEFC\) là hình thoi nên \(I;K\) lần lượt là trung điểm của \(DE\) và \(BF\)
Suy ra \(EI = \dfrac{{DE}}{2};\,FK = \dfrac{{BF}}{2}\) mà \(DE = BF\left( {cmt} \right) \Rightarrow EI = FK\,\,\left( 2 \right)\)
Từ (1) và (2) suy ra tứ giác \(EIFK\) là hình bình hành.
Mà \(AEDF\) là hình thoi nên \(AF \bot DE\) (tính chất hình thoi)\( \Rightarrow \widehat {EIF} = 90^\circ \)
Hình bình hành \(EIFK\) có một góc vuông \(\widehat {EIF} = 90^\circ \) nên \(EIFK\) là hình chữ nhật.
Chọn câu đúng nhất.
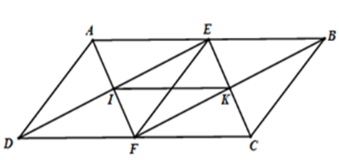
Xét hình bình hành \(ABCD\) có \(E;F\) lần lượt là trung điểm của \(AB;CD\); \(DC = 2BC\) nên
\(AE = EB = BC = CF = DF = AD\) ;\(AB//CD;\,AD//BC\)
Xét tứ giác \(DEBF\) có \(\left\{ \begin{array}{l}EB//DF\\EB = DF\end{array} \right.\) nên \(DEBF\) là hình bình hành (dhnb)
Xét tứ giác \(AEFD\) có \(AE = DF;AE//DF\) nên \(AEFD\) là hình bình hành (dhnb), lại có \(AE = AD\) nên hình bình hành \(AEFD\) là hình thoi.
Tương tự ta cũng có \(EBCF\) là hình thoi. Nhận thấy chưa đủ điều kiện để \(EBCF\) là hình vuông.
Nên A, B đúng, C sai.
Chọn câu đúng nhất.

Xét hình bình hành \(ABCD\) có \(E;F\) lần lượt là trung điểm của \(AB;CD\); \(DC = 2BC\) nên
\(AE = EB = BC = CF = DF = AD\) ;\(AB//CD;\,AD//BC\)
Xét tứ giác \(DEBF\) có \(\left\{ \begin{array}{l}EB//DF\\EB = DF\end{array} \right.\) nên \(DEBF\) là hình bình hành (dhnb)
Xét tứ giác \(AEFD\) có \(AE = DF;AE//DF\) nên \(AEFD\) là hình bình hành (dhnb), lại có \(AE = AD\) nên hình bình hành \(AEFD\) là hình thoi.
Tương tự ta cũng có \(EBCF\) là hình thoi. Nhận thấy chưa đủ điều kiện để \(EBCF\) là hình vuông.
Nên A, B đúng, C sai.
Tìm điều kiện của tam giác $ABC$ để tứ giác $AMCK$ là hình vuông?
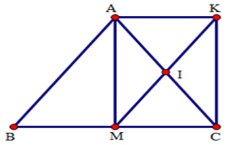
Theo câu trước thì \(AKCM\) là hình chữ nhật.
Để hình chữ nhật $AMCK$ là hình vuông thì $AM = MC$
Mà $AM$ là đường trung tuyến của tam giác cân $ABC$
\( \Rightarrow AM = MC = \dfrac{1}{2}BC \Rightarrow \) Tam giác $ABC$ vuông cân tại $A.$
Tứ giác $AKMB$ là hình gì?
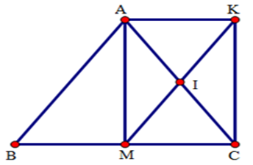
Tứ giác $AMCK$ là hình chữ nhật (theo câu trước)
\( \Rightarrow \) $AK//CM$ \( \Rightarrow \)$AK//BM$ (3)
mà $AK = MC{\rm{ }}(AMCK$ là hình chữ nhật) và $MC = MB$ (gt)
\( \Rightarrow \)$AK = BM$ (4)
Từ (3) và (4) \( \Rightarrow \)Tứ giác $AKMB$ là hình bình hành. (dấu hiệu nhận biết)
Tứ giác $AMCK$ là hình gì?
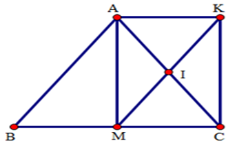
\(\Delta ABC\) cân tại $A$ có $AM$ là trung tuyến nên $AM$ đồng thời là đường cao\( \Rightarrow AM \bot BC \Rightarrow \widehat {AMC} = {90^0}.\) (1)
Xét tứ giác $AMCK$ có: $AC$ cắt $MK$ tại $I,$ mà $AI = IC,MI = IK\;$ (gt)
\( \Rightarrow \) Tứ giác $AMCK$ là hình bình hành (dấu hiệu nhận biết) (2)
Từ (1) và (2) \( \Rightarrow \) $AMCK$ là hình chữ nhật (dấu hiệu nhận biết).
Tứ giác $AMCK$ là hình gì?

\(\Delta ABC\) cân tại $A$ có $AM$ là trung tuyến nên $AM$ đồng thời là đường cao\( \Rightarrow AM \bot BC \Rightarrow \widehat {AMC} = {90^0}.\) (1)
Xét tứ giác $AMCK$ có: $AC$ cắt $MK$ tại $I,$ mà $AI = IC,MI = IK\;$ (gt)
\( \Rightarrow \) Tứ giác $AMCK$ là hình bình hành (dấu hiệu nhận biết) (2)
Từ (1) và (2) \( \Rightarrow \) $AMCK$ là hình chữ nhật (dấu hiệu nhận biết).
Số đo góc $AED$ là:
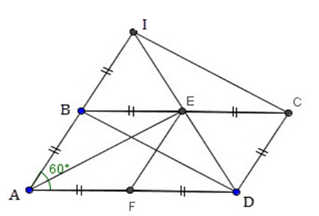
Theo câu trước ta có \(BICD\) là hình chữ nhật lại có \(E\) là trung điểm của \(BC\) (gt) nên \(E\) cũng là trung điểm của \(ID.\)
Mà tam giác \(ADI\) đều (theo câu trước) có \(AE\) là đường trung tuyến nên \(AE\) cũng là đường cao, suy ra \(AE \bot BD \Rightarrow \widehat {AED} = 90^\circ .\)
Tứ giác $BICD$ là hình gì?
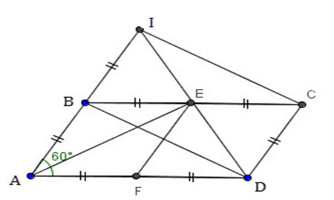
Do $AB//CD$ (giả thiết) nên $BI//CD$
Mặt khác $BI = AB$ (giả thiết); $AB = CD$ (giả thiết)
$ \Rightarrow BI = CD$
Vậy $BICD$ là hình bình hành (dhnb) (1)
Theo giả thiết ta có \(BI = AB = AF = FD \Rightarrow AI = AD\) mà \(\widehat {IAD} = 60^\circ \) (gt) nên tam giác \(ADI\) đều.
Xét tam giác $ADI$ đều có $BD$ là trung tuyến đồng thời là đường cao.
$ \Rightarrow \widehat {DBI} = 90^\circ $ (2)
Từ (1) và (2) suy ra $BICD$ là hình chữ nhật (dấu hiệu nhận biết).
Tứ giác $BICD$ là hình gì?

Do $AB//CD$ (giả thiết) nên $BI//CD$
Mặt khác $BI = AB$ (giả thiết); $AB = CD$ (giả thiết)
$ \Rightarrow BI = CD$
Vậy $BICD$ là hình bình hành (dhnb) (1)
Theo giả thiết ta có \(BI = AB = AF = FD \Rightarrow AI = AD\) mà \(\widehat {IAD} = 60^\circ \) (gt) nên tam giác \(ADI\) đều.
Xét tam giác $ADI$ đều có $BD$ là trung tuyến đồng thời là đường cao.
$ \Rightarrow \widehat {DBI} = 90^\circ $ (2)
Từ (1) và (2) suy ra $BICD$ là hình chữ nhật (dấu hiệu nhận biết).
Hình bình hành $ABCD$ có thêm điều kiện gì thì $EIFK$ là hình vuông ?
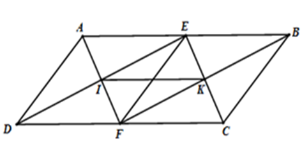
Ta có $EIFK$ là hình chữ nhật (theo câu trước).
Để hình chữ nhật $EIFK$ là hình vuông $ \Leftrightarrow IE = {\rm{IF}}\left( 1 \right)$.
Mà \(I\) là giao điểm hai đường chéo \(DE;AF\) của hình thoi\(AEFD\) nên $IE = \dfrac{1}{2}DE;{\rm{IF = }}\dfrac{1}{2}{\rm{AF}} \Rightarrow {\rm{DE = AF}}$
Mặt khác ta có $AEFD$ là hình thoi (chứng minh ở câu trước) (2).
Từ (1) và (2) $ \Rightarrow AEFD$ là hình vuông $ \Rightarrow AD \bot DC$.
Suy ra hình bình hành \(ABCD\) phải là hình chữ nhật thì \(EIFK\) là hình vuông.
Một tứ giác là hình bình hành nếu nó là:
+ Đáp án A là hình thang cân.
+ Đáp án C là hình thang cân.
+ Đáp án D chưa đủ điều kiện để là hình bình hành.
+ Dựa vào dấu hiệu nhận biết hình bình hành ta thấy một tứ giác là hình bình hành nếu có hai cạnh đối song song và bằng nhau nên đáp án B đúng.
Hình bình hành có hai đường chéo vuông góc là:
Theo dấu hiệu nhận biết hình thoi thì hình bình hành có hai đường chéo vuông góc là hình thoi.
Tứ giác có 2 cạnh đối song song và 2 đường chéo bằng nhau là:
Tứ giác có 2 cạnh đối song song là hình thang. Lại thêm có 2 đường chéo bằng nhau nên tứ giác đó là hình thang cân.
Trong các tứ giác sau, tứ giác nào là hình có \(4\) trục đối xứng?
+) Hình vuông là tứ giác có 4 trục đối xứng.
+) Hình chữ nhật có 2 trục đối xứng là hai đường trung trực của các cạnh.
+) Hình bình hành không có trục đối xứng.
+) Hình thoi có 2 trục đối xứng là 2 đường chéo.
Một tam giác đều có độ dài cạnh bằng $14{\rm{ }}cm$ . Độ dài một đường trung bình của tam giác đó là:
Độ dài một đường trung bình của tam giác là: \(14:2 = 7\,cm.\)
Cho tứ giác $ABCD,$ có \(\widehat A = {70^0},\) \(\widehat B = {120^0},\) \(\widehat D = {50^0},\) Số đo \(\widehat C\) là:
Xét tứ giác \(ABCD\) ta có: $\hat A + \widehat B + \widehat C + \widehat D = {360^0}$
$\begin{array}{l} \Rightarrow \widehat C = {360^0} - \left( {\hat A + \widehat B + \widehat D} \right)\\\,\,\,\,\,\,\,\,\,\,\,\, = {360^0} - \left( {{{70}^0} + {{120}^0} + {{50}^0}} \right)\\\,\,\,\,\,\,\,\,\,\,\,\, = {360^0} - {240^0} = {120^0}.\end{array}$
Hình thang $ABCD$ ($AB\, // \, CD$ ) có số đo góc $D$ bằng ${70^0},$ số đo góc $A$ là:
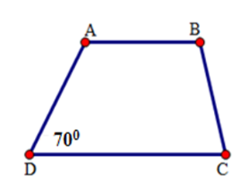
Ta có: \(\widehat A + \widehat D = {180^0}\)
\(\begin{array}{l} \Rightarrow \widehat A = {180^0} - \widehat D\\\,\,\,\,\,\,\,\,\,\,\,\, = {180^0} - {70^0}\\\,\,\,\,\,\,\,\,\,\,\,\,\, = {110^0}\end{array}\)
Một hình thang cân có cạnh bên là $2,5cm;$ đường trung bình là $3\,cm.$ Chu vi của hình thang là:
Tổng độ dài hai đáy là: \(3.2 = 6(cm)\)
Chu vi hình thang là: \(2,5.2 + 6 = 11(cm)\)
Độ dài một cạnh hình vuông bằng $5\,cm.$ Thì độ dài đường chéo hình vuông đó sẽ là:
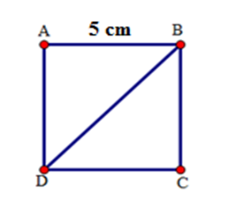
Cho hình vuông $ABCD$ có cạnh bằng $5cm.$
Xét tam giác $ABD$ vuông tại $A,$ theo định lý Pytago ta có:
\(\begin{array}{l}B{D^2} = A{B^2} + A{D^2} = {5^2} + {5^2} = 50\\ \Rightarrow BD = \sqrt {50} = 5\sqrt 2 (cm)\end{array}\)

