Chọn câu đúng.
Hình lăng trụ đứng có hai đáy là những đa giác, các mặt bên là những hình chữ nhật.
Câu nào không đúng về các cạnh bên của hình lăng trụ đứng.
Hình lăng trụ đứng có các mặt bên là hình chữ nhật, các cạnh bên vuông góc với đáy nên chúng song song và bằng nhau.
Chỉ có đáp án D sai.
Có bao nhiêu cạnh vuông góc với mặt phẳng (ADD′A′)?
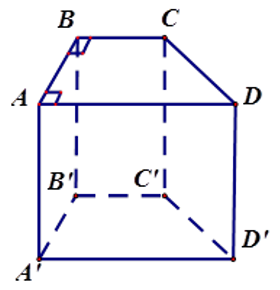
Vì AB⊥AD (do ABCD là hình thang vuông) và AB⊥AA′ (tính chất lăng trụ đứng)
Nên AB⊥(ADD′A′), tương tự ta có: A′B′⊥(ADD′A′)
Do đó AB,A′B′ vuông góc với mp (ADD′A′).
Có bao nhiêu cạnh song song với mặt phẳng (ABB′A′)?
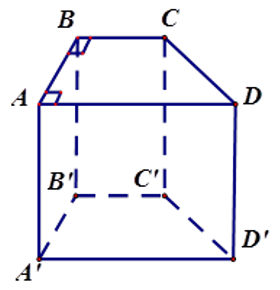
Vì CC′//BB′,DD′//AA′ nên các đường thẳng DD′,CC′ song song với mp (ABB′A′).
Có bao nhiêu cạnh song song với mặt phẳng (ABB′A′)?

Vì CC′//BB′,DD′//AA′ nên các đường thẳng DD′,CC′ song song với mp (ABB′A′).
Cho hình lăng trụ đứng ABC.A′B′C′ có AB=5cm,AC=12cm,BC=13cm. Mặt phẳng nào dưới đây không vuông góc với mặt phẳng (ABB′A′)?
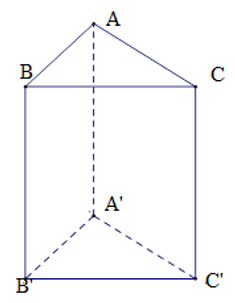
Tam giác ABC có: AB2+AC2=52+122=132=BC2 nên ΔABC vuông tại A (định lý Pytago đảo)
nên AC⊥AB. Do đó A′C′⊥A′B′.
Vì AC vuông góc với hai đường thẳng cắt nhau AB và AA′ nên AC⊥mp(ABB′A′) do đó mp(A′B′C′)⊥mp(ABB′A′).
Vậy có ba mặt phẳng vuông góc với mặt phẳng (ABB′A′) là mp (ABC), mp (A′B′C′), mp (ACC′A′).
Cho hình lăng trụ đứng ABC.A′B′C′ có đáy tam giác ABC vuông tại A. Biết AB=6cm,AC=8cm, AA′=12cm. Diện tích toàn phần của hình lăng trụ đó bằng:
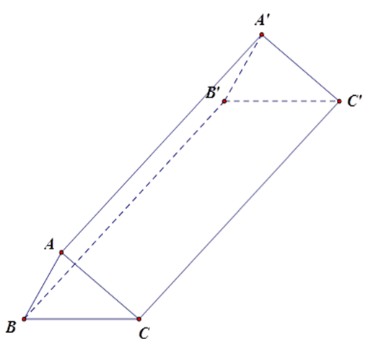
Áp dụng định lý Pytago cho tam giác ABC ta được: BC2=√AB2+AC2=√62+82=10cm.
Ta có:
Chu vi đáy PABC=AB+AC+BC=6+8+10=24cm
Diện tích đáy SABC=AB.AC2=6.82=24cm2.
Diện tích xung quanh của lăng trụ đứng: Sxq=24.12=288cm2.
Diện tích toàn phần: Stp=288+2.24=336cm2.
Một hình hộp chữ nhật kích thước đáy là 10cm và 15cm. Biết diện tích xung quanh bằng tổng diện tích hai đáy. Độ dài chiều cao là:
Đặt AA′=x.
Diện tích xung quanh bằng:
2(10+15).x=50x(cm2)
Tổng diện tích hai đáy bằng: 2.10.15=300(cm2)
Ta có: 50x=300⇔x=6.
Vậy chiều cao bằng 6cm.
Cho hình lăng trụ tam giác đều ABC.A′B′C′ có chiều cao bằng 2cm. Biết các mặt bên của hình lăng trụ là những hình vuông. Tính diện tích xung quanh của hình lăng trụ.
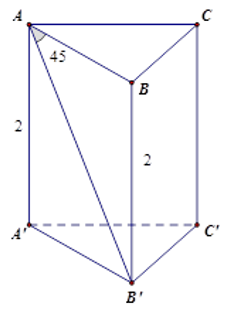
Vì ABB′A′ là hình vuông nên AB=BB′=2cm.
Vì tam giác ABC đều nên chu vi đáy bằng 3AB=3.2=6cm.
Diện tích xung quanh bằng 6.2=12(cm2).
Một hình hộp chữ nhật có diện tích xung quanh bằng 100cm2, chiều cao bằng 5cm. Tìm các kích thước của đáy để hình hộp chữ nhật có thể tích lớn nhất.
Gọi a và b là các kích thước của đáy.
Ta có: V=5ab nên V lớn nhất ⇔ ab lớn nhất
Sxq=100 nên 2(a+b).5=100 hay a+b=10.
Ta có: ab=a(10−a)=−a2+10a=−(a−5)2+25≤25.
Suy ra V=5ab≤5.25=125.
Thể tích lớn nhất bằng 125cm3 khi a=b=5, tức là các cạnh đáy bằng 5 cm.
Một hình lăng trụ đứng có đáy là hình thoi với các đường chéo của đáy bằng 24cm và 10cm. Diện tích toàn phần của hình lăng trụ bằng 1020cm2. Tính chiều cao của hình lăng trụ.
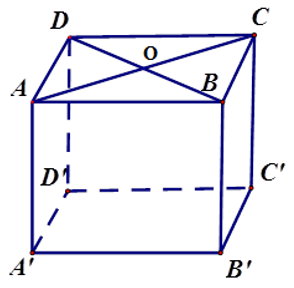
Vì đáy ABCD là hình thoi nên diện tích đáy bằng: 24.10:2=120(cm2)
Từ đó diện tích xung quanh: Sxq=1020−120.2=780(cm2)
Vì ABCD là hình thoi nên AB⊥CD;OD=BD2=242=12cm; OA=AC2=102=5cm.
Nên độ dài cạnh đáy bằng AD=√OA2+OD2=√52+122=13(cm) (định lý Pytago)
Chu vi đáy bằng: 13.4=52(cm)
Chiều cao hình lăng trụ bằng:
780:52=15(cm).
Một hình hộp chữ nhật có đường chéo bằng 3dm, chiều cao 2dm, diện tích xung quanh bằng 12dm2. Diện tích toàn phần của hình hộp chữ nhật là:
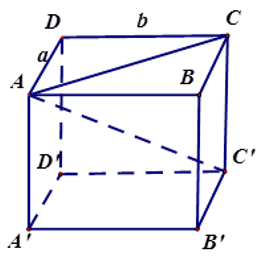
Hình hộp chữ nhật ABCD.A′B′C′D′ có: AC′=3dm;AC=2dm.
Xét tam giác ACC′ vuông tại C, theo định lý Pytago ta có: AC2=C′A2−C′C2=32−22=5.
Vì diện tích xung quanh là 12dm2 nên chu vi đáy bằng 12:2=6(dm)
Đặt AD=a,DC=b
Vì chu vi đáy là 6dm⇒ 2(a+b)=6⇔a+b=3 (1) và a2+b2=AC2=5 (2)
(định lý Pyatgo cho tam giác vuôngADC)
Từ (1) và (2) suy ra a2+(3−a2)=5
Rút gọn được a2−3a+2=0 hay (a−1)(a−2)=0
Giả sử a≥b thì ta tìm được: a = 2 suy ra b = 1.
Diện tích toàn phần của hình hộp chữ nhật bằng: 12+2.1.2=16(dm3).
Tính thể tích của hình lăng trụ đứng có chiều cao 20cm, đáy là một tam giác cân có cạnh bên bằng 5cm và cạnh đáy bằng 8cm.
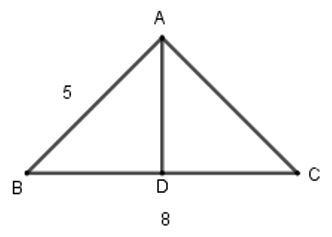
Gọi D là trung điểm của BC thì AD là trung tuyến cũng là đường cao trong tam giác ⇒DB=DC=82=4(cm) và AD⊥BC.
Tam giác ADC vuông tại D nên AD2+DC2=AC2⇔AD2+42=52⇔AD2=9⇔AD=3
Diện tích đáy: S=3.82=12(cm2).
Thể tích lăng trụ đứng là: V=S.h=12.20=240cm3.
Cho lăng trụ đứng có kích thước như hình vẽ.
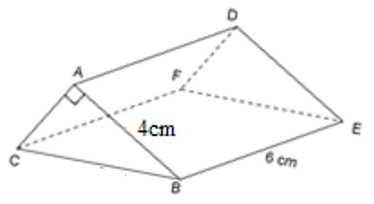
Biết thể tích hình lăng trụ bằng 36cm3, độ dài cạnh BC là:
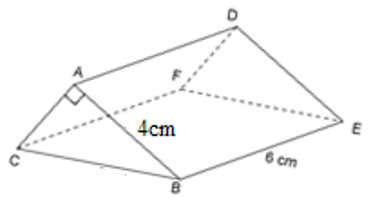
Diện tích tam giác ABC là: S=36:6=6(cm2).
Độ dài cạnh AC là: 2SAB=2.64=3(cm).
Tam giác ABC vuông tại A nên BC2=AB2+AC2=42+32=25⇒BC=5(cm).
Cho một hình lăng trụ đứng có thể tích V, diện tích đáy là S, chiều cao hình lăng trụ được tính theo công thức:
Ta có: V=Sh⇒h=VS.
Tính thể tích của hình lăng trụ đứng sau:
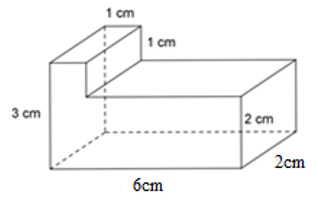
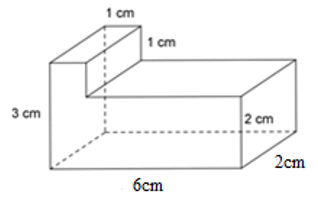
Hình lăng trụ đứng đã cho được tạo thành từ 2 hình hộp chữ nhật. Hình hộp chữ nhật thứ nhất có kích thước là
3cm,1cm,2cm; hình hộp chữ nhật thứ hai có kích thước là: 2cm,5cm,2cm.
Thể tích hình hộp chữ nhật thứ nhất là: V1=3.1.2=6cm3
Thể tích hình hộp chữ nhật thứ hai là: V2=2.5.2=20cm3
Thể tích hình lăng trụ đứng là: V=V1+V2=6+20=26cm3
Một lăng trụ đứng có đáy là hình chữ nhật có các kích thước 3cm, 8cm. Chiều cao của hình lăng trụ đứng là 2cm. Thể tích của hình lăng trụ đứng là:
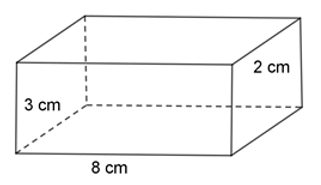
Thể tích của hình lăng trụ đứng là: V=8.3.2=48cm3.
Tính thể tích nhà kho có dạng hình lăng trụ đứng ngũ giác với các kích thước được đo bằng mét.
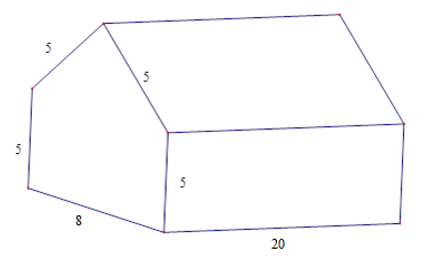
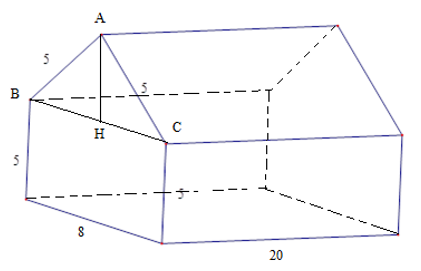
Gọi H là trung điểm BC⇒AH⊥BC . Ta có BH=4;AB=5m
Áp dụng định lí Py-ta-go ta có: AH=√AB2−BH2=3m
Diện tích đáy của hình lăng trụ bằng:
S=5.8+8.32=52(m2)
Thể tích nhà kho bằng:
V=52.20=1040(m3).
Thể tích hình lăng trụ đứng là:
Thể tích hình lăng trụ đứng ABC.DEF là: V=Sd.h=24.12=288cm3.
Diện tích toàn phần của lăng trụ là:
Diện tích xung quanh của hình lăng trụ ABC.DEF là:
Sxq=(6+8+10).12=288cm2
Diện tích đáy ABC của hình lăng trụ ABC.DEF là:
Sd=12AB.BC=12.6.8=24cm2
Diện tích toàn phần của hình lăng trụ ABC.DEF là:
Stp=Sxq+2.Sd=288+2.24=336cm2.

