Trong các đơn thức sau đơn thức nào đồng dạng với đơn thức \( - 2{x^3}y\)?
Ta có: \({x^2}y\left( { - 5x} \right) = - 5{x^3}y\) đồng dạng với \( - 2{x^3}y.\)
Số nghiệm của đa thức \(P\left( x \right) + Q\left( x \right)\) là:
Sử dụng kết quả câu trước \(\,P\left( x \right) + Q\left( x \right) = \,{x^2} + x + \dfrac{3}{4}\).
Xét: \(P\left( x \right) + Q\left( x \right) = 0\)
\(\begin{array}{l} \Leftrightarrow \,{x^2} + x + \dfrac{3}{4} = \left( {{x^2} + 2.\dfrac{1}{2}.x + \dfrac{1}{4}} \right) + \dfrac{2}{4}\\ = {\left( {x + \dfrac{1}{2}} \right)^2} + \dfrac{1}{2} \ge \dfrac{1}{2}\,\,\,\,\,\,\forall x\end{array}\).
Vậy \(P\left( x \right) + Q\left( x \right)\) luôn không có nghiệm.
Tính \(P\left( x \right) + Q\left( x \right);\,P\left( x \right) - Q\left( x \right).\)
Theo câu trước ta có: \(P\left( x \right) = \,4{x^4} + 4{x^3} + 7{x^2} + 1\,;\) \(Q\left( x \right) = \, - 4{x^4} - 4{x^3} - 6{x^2} + x - \dfrac{1}{4}.\)
Suy ra:
\( + )\,P\left( x \right) + Q\left( x \right) = \left( {4{x^4} - 4{x^4}} \right) + \left( {4{x^3} - 4{x^3}} \right) + \left( {7{x^2} - 6{x^2}} \right) + x - \dfrac{1}{4} + 1\)\( \Leftrightarrow \,P\left( x \right) + Q\left( x \right) = \,{x^2} + x + \dfrac{3}{4}\)
\( + )P\left( x \right) - Q\left( x \right) = \left( {4{x^4} - \left( { - 4{x^4}} \right)} \right) + \left( {4{x^3} - \left( { - 4{x^3}} \right)} \right) + \left( {7{x^2} - \left( { - 6{x^2}} \right)} \right) - x + \dfrac{1}{4} + 1\)\( \Leftrightarrow P\left( x \right) - Q\left( x \right)\, = 8{x^4} + 8{x^3} + 13{x^2} - x + \dfrac{5}{4}\).
Vậy \(\,P\left( x \right) + Q\left( x \right) = \,{x^2} + x + \dfrac{3}{4};\)\(P\left( x \right) - Q\left( x \right)\, = 8{x^4} + 8{x^3} + 13{x^2} - x + \dfrac{5}{4}\).
Thu gọn và sắp xếp các đa thức theo lũy thừa giảm dần của biến.
Ta có:
\(\begin{array}{l}P\left( x \right)\,\,\, = 1 + 3{x^4} + 2{x^2} + {x^4} + {x^3} + 5{x^2} + 3{x^3}\\\, = \left( {3{x^4} + {x^4}} \right) + \left( {{x^3} + 3{x^3}} \right) + \left( {2{x^2} + 5{x^2}} \right) + 1\,\\ = \,4{x^4} + 4{x^3} + 7{x^2} + 1\,\end{array}\)
\(\begin{array}{l}Q\left( x \right) = - 4{x^4} - 2{x^2} - 4{x^3} + 2x - 4{x^2} - x - \dfrac{1}{4}\\ = - 4{x^4} - 4{x^3} + \left( { - 2{x^2} - 4{x^2}} \right) + \left( {2x - x} \right) - \dfrac{1}{4}\\ = \, - 4{x^4} - 4{x^3} - 6{x^2} + x - \dfrac{1}{4}\end{array}\)
Vậy \(P\left( x \right) = \,4{x^4} + 4{x^3} + 7{x^2} + 1\,;\)\(Q\left( x \right) = \, - 4{x^4} - 4{x^3} - 6{x^2} + x - \dfrac{1}{4}.\)
Thu gọn và sắp xếp các đa thức theo lũy thừa giảm dần của biến.
Ta có:
\(\begin{array}{l}P\left( x \right)\,\,\, = 1 + 3{x^4} + 2{x^2} + {x^4} + {x^3} + 5{x^2} + 3{x^3}\\\, = \left( {3{x^4} + {x^4}} \right) + \left( {{x^3} + 3{x^3}} \right) + \left( {2{x^2} + 5{x^2}} \right) + 1\,\\ = \,4{x^4} + 4{x^3} + 7{x^2} + 1\,\end{array}\)
\(\begin{array}{l}Q\left( x \right) = - 4{x^4} - 2{x^2} - 4{x^3} + 2x - 4{x^2} - x - \dfrac{1}{4}\\ = - 4{x^4} - 4{x^3} + \left( { - 2{x^2} - 4{x^2}} \right) + \left( {2x - x} \right) - \dfrac{1}{4}\\ = \, - 4{x^4} - 4{x^3} - 6{x^2} + x - \dfrac{1}{4}\end{array}\)
Vậy \(P\left( x \right) = \,4{x^4} + 4{x^3} + 7{x^2} + 1\,;\)\(Q\left( x \right) = \, - 4{x^4} - 4{x^3} - 6{x^2} + x - \dfrac{1}{4}.\)
Chọn câu đúng.
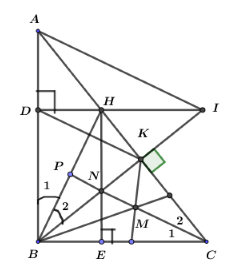
Xét tam giác \(HBC\) ta có:
\(BK \bot HC\left( {Gt} \right) \Rightarrow BK\) là đường cao xuất phát từ đỉnh \(B\) của tam giác \(HBC\).
Ta có:
\(\begin{array}{l}DI \bot AB\left( {GT} \right)\\BC \bot AB\left( {gt} \right)\,\,\,\,\,\, \Rightarrow \angle DIB = \angle KBC\,\left( {so\,le\,trong} \right)\\ \Rightarrow DI//BC\end{array}\)
Mà:
\(\begin{array}{l}\angle C + \angle KBC = {90^0}\\\angle DBI + \angle DIB = {90^0}\\ \Rightarrow \angle C = \angle DBI\\ \Rightarrow \angle {B_1} = \angle {B_2} = \angle {C_1} = \angle {C_2}\,\,\,\left( 1 \right)\end{array}\)
Kéo dài CN cắt BH tại P, ta chứng minh CP là đường cao kẻ từ đỉnh C của tam giác \(HBC\).
Ta có:
\(\begin{array}{l} + )\,\angle C + \angle KBC = {90^0}\\ + )\angle {C_1} + \angle {C_2} + \angle KBC = {90^0}\end{array}\).
Mà \(\angle {C_2} = \angle {B_2}\,\,\left( {cmt} \right) \Rightarrow \angle {C_1} + \angle KBC + \angle {B_2} = \angle BPC = {90^0}\) Hay \(CP \bot CH\).
Trong tam giác \(HBC\) có: CN là đường cao, BN là đường cao.
\( \Rightarrow \) N là trực tâm của \(\Delta HBC\).
Chọn câu đúng nhất.
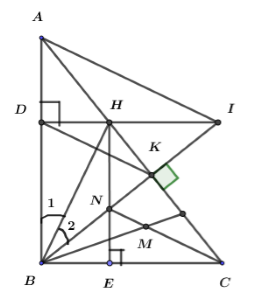
+) Vì \(\Delta BHK = \Delta BHD\) nên \(HK = HD\) (cạnh tương ứng)
Xét hai tam giác \(\Delta ADH;\,\Delta IKH\)
Có:
+) \(\angle DHA = \angle KHI\) (đối đỉnh)
+) \(HK = HD\)(cmt)
+) \(\angle ADH = \angle IKH = {90^0}\)
\( \Rightarrow \Delta ADH = \,\,\Delta IKH\) (g.c.g)
\(IK = AD\) (cạnh tương ứng)
+) Trong tam giác \(ABC\) có:
\(\begin{array}{l}AB = AD + DB\\BI = BK + KI\end{array}\)
Mà \(AD = IK\,\) (do \(\Delta ADH = \Delta IKH\left( {cmt} \right)\))
\(DB = BK\) (do \(\Delta BHK = \Delta BHD\))
\( \Rightarrow AB = BI\)
\( \Rightarrow \Delta ABI\) là tam giác cân tại B. \( \Rightarrow \angle BAI = \angle BIA\)
Trong một tam giác cân, tia phân giác ứng với cạnh đáy chính là đường cao
\( \Rightarrow BH \bot AI\,\,\left( 1 \right)\)
Mà \(\Delta BDK\) cũng cân tại B (do \(BD = BK\left( {do\,\Delta BDH = \Delta BKH} \right)\)
\( \Rightarrow BH \bot DK\,\,\left( 2 \right)\) (do BH là đường phân giác góc B)
Từ (1) và (2) \( \Rightarrow DK//AI\) (do cùng vuông góc với \(BH\))
Vậy \(DK//AI\).
Chọn câu đúng.
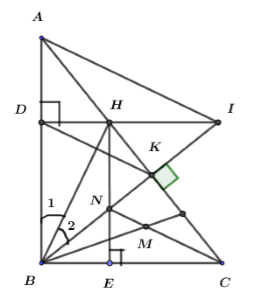
\(\Delta BHK = \Delta BHD\)
Vì BK là đường cao của tam giác \(\Delta ABC\) nên \(BK \bot AC\)
Xét hai tam giác vuông \(BHK\) và \(\Delta BHD\) ta có:
\(\angle {B_1} = \angle {B_2}\) (do BH là đường phân giác của góc \(\angle ABK\left( {H \in AC} \right).\)
Cạnh BH chung
\( \Rightarrow \Delta BHK = \Delta BHD\) (cạnh huyền-góc nhọn)
Chọn câu đúng.

\(\Delta BHK = \Delta BHD\)
Vì BK là đường cao của tam giác \(\Delta ABC\) nên \(BK \bot AC\)
Xét hai tam giác vuông \(BHK\) và \(\Delta BHD\) ta có:
\(\angle {B_1} = \angle {B_2}\) (do BH là đường phân giác của góc \(\angle ABK\left( {H \in AC} \right).\)
Cạnh BH chung
\( \Rightarrow \Delta BHK = \Delta BHD\) (cạnh huyền-góc nhọn)
Có bao nhiêu đa thức trong 4 biểu thức sau: \(2{x^2} - 3xy;\,\) \(2{x^2} - 3x + 1;\,\)\( - 3xy\) và \(\dfrac{{ - 1}}{{2x}}\)?
Trong 4 biểu thức trên chỉ có biểu thức \(\dfrac{{ - 1}}{{2x}}\) không phải đa thức.
Vậy có 3 đa thức trong 4 biểu thức trên.
Bộ ba độ dài nào sau đây không phải là độ dài ba cạnh của một tam giác?
Xét đáp án D có: \(4 - 3 < 7 = 4 + 3\) không thỏa mãn bất đẳng thức tam giác nên bô ba độ dài \({\rm{7cm}},{\rm{ 4cm, 3cm}}\) không là ba cạnh của tam giác.
Bậc của đa thức \({x^{100}} - 2{x^5} - 2{x^3} + 3{x^4} + x - 2018 + 2{x^5} - {x^{100}} + 1\) là:
Ta có:
\(\begin{array}{l}{x^{100}} - 2{x^5} - 2{x^3} + 3{x^4} + x - 2018 + 2{x^5} - {x^{100}} + 1\\ = \left( {{x^{100}} - {x^{100}}} \right) + \left( { - 2{x^5} + 2{x^5}} \right) + 3{x^4} - 2{x^3} + x - 2018 + 1\\ = 3{x^4} - 2{x^3} + x - 2017\end{array}\).
\( \Rightarrow \) bậc của đa thức là: 4.
Tìm x biết \(\dfrac{{6x + 3}}{5} = 3\)?
Ta có:
\(\begin{array}{l}\dfrac{{6x + 3}}{5} = 3\\ \Leftrightarrow 6x + 3 = 3.5\\ \Leftrightarrow 6x + 3 = 15\\ \Leftrightarrow 6x = 15 - 3\\ \Leftrightarrow 6x = 12\\ \Leftrightarrow x = 2\end{array}\).
Biết \({x^2}-16 = 0\) thì giá trị của \(x\) là:
Ta có: \({x^2} - 16 = 0 \Leftrightarrow {x^2} = 16\)\( \Leftrightarrow {x^2} = {4^2} \Leftrightarrow \left[ \begin{array}{l}x = 4\\x = - 4\end{array} \right.\)
Vậy \(x = 4;x = - 4.\)
Cho \(\Delta ABC\) vuông tại \(A\) có: \(AB = 6cm;{\rm{ }}AC = 8cm\) thì \(BC = ...?\)
Xét \(\Delta ABC\) vuông tại \(A\), theo định lý Pytago ta có: \(B{C^2} = A{B^2} + A{C^2} \Leftrightarrow B{C^2} = {6^2} + {8^2}\)
\( \Leftrightarrow B{C^2} = 36 + 64 = 100 \Rightarrow BC = 10cm\).
Vậy \(BC = 10cm.\)
Biểu thức sau \(9{x^2} - 6x + 1\;\) được viết dưới dạng bình phương một hiệu là:
Ta có: \(9{x^2} - 6x + 1\; = {\left( {3x} \right)^2} - 2.3x + 1 = {\left( {3x - 1} \right)^2}\).
Giá trị của đa thức \(P = 2{x^3} - 3{y^2} - 2xy\) khi \(x = - 2;y = - 3\) là:
Thay các giá trị \(x = - 2;y = - 3\) vào biểu thức của \(P\) ta được:
\(\begin{array}{l}P = 2{x^3} - 3{y^2} - 2xy\\\,\,\,\,\, = 2. {\left( { - 2} \right)^3} - 3. {\left( { - 3} \right)^2} - 2.\left( { - 2} \right).\left( { - 3} \right)\\\,\,\,\,\, = - 16\, - 27\, - 12\\\,\,\,\,\, = \, - 55\end{array}\).
Khẳng định nào sau đây là sai?
a) Đúng. Số 0 được coi là đơn thức không có bậc.
b) Đúng. Trong một tam giác, góc đối diện với cạnh lớn hơn là góc lớn hơn.
c) Sai. Vì trong một tam giác, trọng tâm là giao điểm của ba đường trung tuyến.
d) Đúng. Độ dài một cạnh của một tam giác đều nhỏ hơn nửa chu vi của tam giác ấy.
Áp dụng tính bất đẳng thức tam giác. Giả sử tam giác có 3 cạnh a, b, c.
Thật vậy, ta có:
\(\begin{array}{l}a < b + c\\ \Rightarrow \dfrac{a}{2} < \dfrac{{b + c}}{2}\\ \Rightarrow \dfrac{a}{2} + \dfrac{a}{2} < \dfrac{a}{2} + \dfrac{{b + c}}{2}\\ \Rightarrow \,a\, < \,\dfrac{{a + b + c}}{2}\end{array}\).
Tương tự ta cũng chứng minh được: \(b < \dfrac{{a + b + c}}{2};\,\,c < \dfrac{{a + b + c}}{2}\).
Vậy: Độ dài một cạnh của một tam giác đều nhỏ hơn nửa chu vi của tam giác ấy.
Tính giá trị biểu thức \(\left( {\dfrac{1}{2} - \dfrac{{13}}{{14}}} \right):\dfrac{5}{7} - \left( { - \dfrac{2}{{21}} + \dfrac{1}{7}} \right):\dfrac{5}{7}\) ta được:
Ta có: \(\left( {\dfrac{1}{2} - \dfrac{{13}}{{14}}} \right):\dfrac{5}{7} - \left( { - \dfrac{2}{{21}} + \dfrac{1}{7}} \right):\dfrac{5}{7}\)\( = \left[ {\dfrac{1}{2} - \dfrac{{13}}{{14}} - \left( { - \dfrac{2}{{21}} + \dfrac{1}{7}} \right)} \right]:\dfrac{5}{7}\)
\( = \left( {\dfrac{1}{2} - \dfrac{{13}}{{14}} + \dfrac{2}{{21}} - \dfrac{1}{7}} \right):\dfrac{5}{7}\) \( = \left( {\dfrac{{21}}{{42}} - \dfrac{{39}}{{42}} + \dfrac{4}{{42}} - \dfrac{6}{{42}}} \right):\dfrac{5}{7}\)
\( = \dfrac{{21 - 39 + 4 - 6}}{{42}}.\dfrac{7}{5} = \dfrac{{ - 20}}{{42}}.\dfrac{7}{5} = - \dfrac{2}{{3}}\).
Tìm \(x\) biết \(\left( {x + 1} \right)\left( {x + 3} \right) - x\left( {x + 2} \right) = 7\).
Ta có: \(\left( {x + 1} \right)\left( {x + 3} \right) - x\left( {x + 2} \right) = 7\;\)
\( \Leftrightarrow x. x + x. 3 + 1. x + 1. 3 - x. x - x. 2 = 7\)
\(\begin{array}{l} \Leftrightarrow {x^2} + 3x + x + 3 - {x^2} - 2x = 7\\ \Leftrightarrow 2x = 4\\ \Leftrightarrow x = 2\end{array}\)
Vậy \(x = 2.\)

