Tứ giác \(AMBM'\) là hình gì?
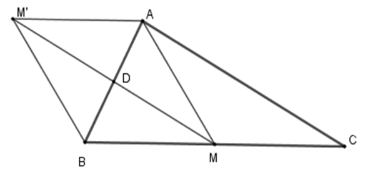
Vì \(M'\) đối xứng $M$ qua $D$ nên \(DM = DM'\) (1).
$M,D$ lần lượt là trung điểm của $BC,AB$ nên $MD$ là đường trung bình của $\Delta ABC$ . Suy ra \(MD{\rm{//}}AC\) (2).
Mặt khác $\Delta ABC$vuông ở $A$ nên \(AB \bot AC\)(2).
Từ (1) và (2) suy ra \(DM \bot AB \Rightarrow MM' \bot AB\).
Vì $D$ là trung điểm của $AB$(gt) và $D$ là trung điểm của \(MM'\) nên tứ giác $AMBM'$là hình bình hành. Mặt khác \(MM' \bot AB\)nên $AMBM'$ là hình thoi.
Cho \(BC = 4\,cm\) . Tính chu vi tứ giác \(AMBM'\).
Vì \(BC = 4\,cm\) nên \(BM = \dfrac{{BC}}{2} = 2\,cm\) .
Chu vi tứ giác $AMBM'$ bằng \(4.BM = 4.2 = 8\,cm\).
Tứ giác \(AMBM'\) là hình gì?

Vì \(M'\) đối xứng $M$ qua $D$ nên \(DM = DM'\) (1).
$M,D$ lần lượt là trung điểm của $BC,AB$ nên $MD$ là đường trung bình của $\Delta ABC$ . Suy ra \(MD{\rm{//}}AC\) (2).
Mặt khác $\Delta ABC$vuông ở $A$ nên \(AB \bot AC\)(2).
Từ (1) và (2) suy ra \(DM \bot AB \Rightarrow MM' \bot AB\).
Vì $D$ là trung điểm của $AB$(gt) và $D$ là trung điểm của \(MM'\) nên tứ giác $AMBM'$là hình bình hành. Mặt khác \(MM' \bot AB\)nên $AMBM'$ là hình thoi.
Tứ giác \(AMBM'\) là hình gì?

Vì \(M'\) đối xứng $M$ qua $D$ nên \(DM = DM'\) (1).
$M,D$ lần lượt là trung điểm của $BC,AB$ nên $MD$ là đường trung bình của $\Delta ABC$ . Suy ra \(MD{\rm{//}}AC\) (2).
Mặt khác $\Delta ABC$vuông ở $A$ nên \(AB \bot AC\)(2).
Từ (1) và (2) suy ra \(DM \bot AB \Rightarrow MM' \bot AB\).
Vì $D$ là trung điểm của $AB$(gt) và $D$ là trung điểm của \(MM'\) nên tứ giác $AMBM'$là hình bình hành. Mặt khác \(MM' \bot AB\)nên $AMBM'$ là hình thoi.
Điền từ thích hợp vào chỗ trống: “Tứ giác có hai đường chéo… là hình thoi”
+ Tứ giác có hai đường chéo giao nhau tại trung điểm mỗi đường là hình bình hành.
+ Hình bình hành có hai đường chéo vuông góc là hình thoi.
Nên tứ giác có hai đường chéo giao nhau tại trung điểm mỗi đường và vuông góc với nhau là hình thoi.
Điền cụm từ thích hợp vào chỗ trống: “Hình thoi có hai đường chéo…”
Hình thoi có tất cả các tính chất của hình bình hành:
+ Các cạnh đối song song và bằng nhau, các góc đối bằng nhau.
+ Hai đường chéo giao nhau tại trung điểm mỗi đường.
Ngoài ra còn có:
+ Hai đường chéo vuông góc với nhau.
+ Hai đường chéo là các đường phân giác của các góc của hình thoi.
Tứ giác dưới đây là hình thoi theo dấu hiệu nào?
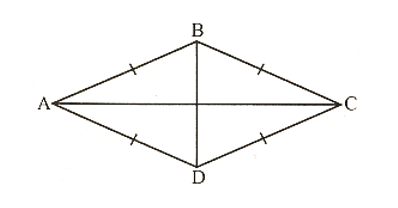
Tứ giác có 4 cạnh bằng nhau là hình thoi nên A đúng.
Hình thoi có chu vi bằng \(36\)\(cm\) thì độ dài cạnh của nó bằng.
Gọi cạnh của hình thoi là \(a\,\,cm\,\left( {a > 0} \right)\).
Vì hình thoi có bốn cạnh bằng nhau nên chu vi hình thoi là \(4a = 36 \Leftrightarrow a = 9\,cm\).
Vậy cạnh hình thoi có độ dài là \(9\,cm\).
Cho hình thoi \(ABCD\) có chu vi bằng \(24\,cm\), đường cao \(AH\) bằng \(3\,cm\). Tính \(\widehat {DCA}\).
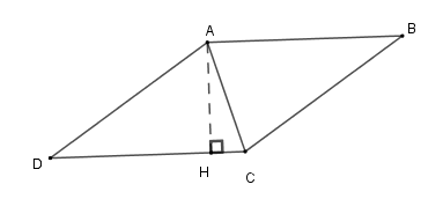
Vì chu vi hình thoi là \(24\,cm\) nên cạnh hình thoi có độ dài \(24:\,4 = 6\,cm\). Suy ra \(AD = 6\,cm\).
Xét tam giác \(AHD\) vuông tại \(H\) có: \(AH = \dfrac{1}{2}AD \Rightarrow \widehat {ADH} = 30^\circ \) (tính chất)
Suy ra \(\widehat {DAB} = 180^\circ - \widehat {ADC} = 180^\circ - 30^\circ = 150^\circ \) (vì \(ABCD\) là hình thoi)
Nên hình thoi \(ABCD\) có: \(\,\widehat A = \widehat C = 150^\circ \) (vì hai góc đối bằng nhau).
Lại có: \(CA\) là tia phân giác \(\widehat {DCB}\) (tính chất hình thoi) nên \(\widehat {DCA} = \dfrac{1}{2}\widehat {DCB} = \dfrac{1}{2}. 150^\circ = 75^\circ \).
Cho hình bình hành \(ABCD.\) Gọi E, F là trung điểm của các cạnh \(AD\) và \(BC.\) Các đường BE, DE cắt các đường chéo AC tại P và Q. Tứ giác EPFQ là hình thoi nếu góc ACD bằng:
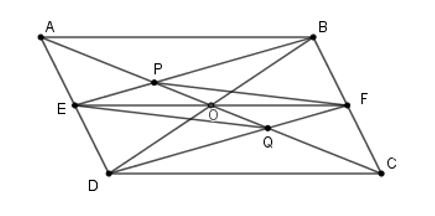
Gọi \(O\) là giao điểm của hai đường chéo \(AC\) và \(BD\)
Vì \(ABCD\) là hình hình hành nên \(O\) là trung điểm của \(AC,BD.\)
Xét tứ giác \(EDFB\) có \(\left\{ \begin{array}{l}ED//FB\\ED = FB\left( { = \dfrac{1}{2}AD} \right)\end{array} \right.\) nên \(EDFB\) là hình bình hành, suy ra \(\left\{ \begin{array}{l}BE = DF\\BE//DF\end{array} \right.\)
Xét tam giác \(ABD\) có \(P\) là giao điểm hai đường trung tuyến nên \(P\) là trọng tâm \(\Delta ABD \Rightarrow EP = \dfrac{1}{3}BE\)
Xét tam giác \(CBD\) có \(Q\) là giao điểm hai đường trung tuyến nên \(Q\) là trọng tâm \(\Delta CBD \Rightarrow QF = \dfrac{1}{3}DF\)
Mà \(BE = DF\left( {cmt} \right) \Rightarrow EP = QF\)
Xét tứ giác \(EPFQ\) có \(\left\{ \begin{array}{l}EP = QF\\EP//QF\end{array} \right. \Rightarrow EPFQ\) là hình bình hành.
Để hình bình hành \(EPFQ\) là hình thoi thì \(EF \bot PQ\).
Mà \(EF//CD\) (do \(E\) là trung điểm \(AD,F\) là trung điểm \(BC\)).
Nên \(PQ \bot CD\) hay \(AC \bot CD \Rightarrow \widehat {ACD} = 90^\circ \).
Cho hình thoi có độ dài hai đường chéo là \(12\,cm\) và \(16\,cm\). Tính độ dài cạnh hình thoi.
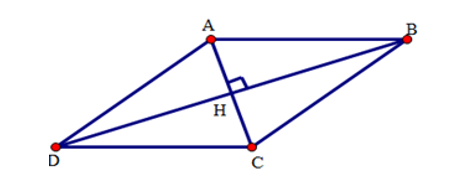
Giả sử ABCD là hình thoi có hai đường chéo \(AC = 12cm,BD = 16cm.\)
Do \(ABCD\) là hình thoi nên:
\(AC \bot BD;\,\,AH = \dfrac{1}{2}AC = \dfrac{1}{2}.12 = 6\left( {cm} \right);\,\,HB = \dfrac{1}{2}BD = \dfrac{1}{2}. 16 = 8\left( {cm} \right).\)
Xét tam giác \(AHB\) vuông tại \(H\) ta có: \(A{B^2} = A{H^2} + H{B^2} = {6^2} + {8^2} = 36 + 64 = 100\).
Suy ra \(AB = 10\,cm\).
Cho \(OC = 4;OH = 3\). Tính chu vi tứ giác \(AHCG\).
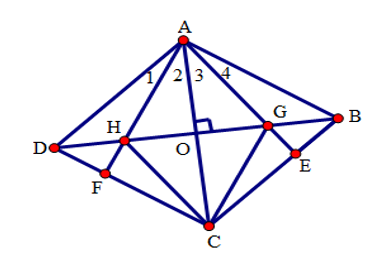
Vì \(OC = 4;OH = 3\) nên \(CH = \sqrt {O{H^2} + O{C^2}} = \sqrt {{3^2} + {4^2}} = 5\) (định lý Pytago).
Vì \(AHCG\) là hình thoi (theo câu trước) nên chu vi tứ giác \(AHCG\) bằng \(4. CH = 4. 5 = 20\,cm\).
Tứ giác \(AGCH\) là hình gì?
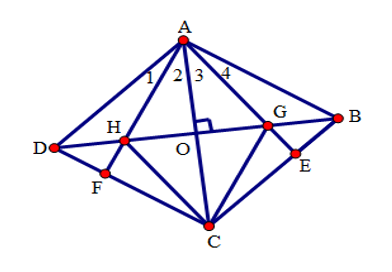
Gọi O là giao điểm của AC và BD thì \(AC \bot BD\) (do O là giao điểm của hai đường chéo của hình thoi)
Áp dụng định nghĩa, tính chất về góc và giả thiết vào hình thoi ABCD, ta được:
\(AB = AD,\widehat {\,\,B} = \widehat D,\,\,BE = DF.\)
Từ đó suy ra \(\Delta ABE = \Delta ADF(c.g.c)\)
Suy ra \(\widehat {{A_1}} = \widehat {{A_4}}\) (hai góc tương ứng).
Mà AC là phân giác của \(\widehat A \Rightarrow \widehat {{A_2}} = \widehat {{A_3}}.\) (1)
Do đó AO là phân giác của \(\widehat {HAG}.\)
Xét tam giác AGH có AO là đường cao, đồng thời là đường phân giác nên tam giác AGH cân tại A.
Suy ra: HO = OG (2)
Do ABCD là hình thoi nên AO = OC (tính chất đường chéo của hình thoi) (3)
Từ (1), (2), (3) suy ra: AHCG là hình thoi.
Tứ giác \(AGCH\) là hình gì?

Gọi O là giao điểm của AC và BD thì \(AC \bot BD\) (do O là giao điểm của hai đường chéo của hình thoi)
Áp dụng định nghĩa, tính chất về góc và giả thiết vào hình thoi ABCD, ta được:
\(AB = AD,\widehat {\,\,B} = \widehat D,\,\,BE = DF.\)
Từ đó suy ra \(\Delta ABE = \Delta ADF(c.g.c)\)
Suy ra \(\widehat {{A_1}} = \widehat {{A_4}}\) (hai góc tương ứng).
Mà AC là phân giác của \(\widehat A \Rightarrow \widehat {{A_2}} = \widehat {{A_3}}.\) (1)
Do đó AO là phân giác của \(\widehat {HAG}.\)
Xét tam giác AGH có AO là đường cao, đồng thời là đường phân giác nên tam giác AGH cân tại A.
Suy ra: HO = OG (2)
Do ABCD là hình thoi nên AO = OC (tính chất đường chéo của hình thoi) (3)
Từ (1), (2), (3) suy ra: AHCG là hình thoi.
Tứ giác \(ABCD\) có \(AB = CD.\) Gọi \(M,N\) theo thứ tự là trung đểm của \(BC,AD.\) Gọi \(I,K\) theo thứ tự là trung điểm của \(AC,BD.\) Chọn câu đúng nhất.
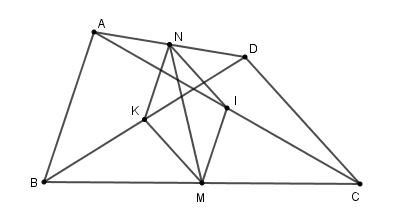
Từ giả thiết ta có: \(KM;IM;IN;KN\) lần lượt là các đường trung bình của các tam giác \(BCD,CAB,ADC,DBA\). (định nghĩa đường trung bình).
Đặt \(BA = CD = 2a\).
Áp dụng định lý đường trung bình và giả thiết vào bốn tam giác trên ta được:
\(MK = \dfrac{1}{2}CD = a;IM = \dfrac{1}{2}AB = a;NI = \dfrac{1}{2}CD = a;KN = \dfrac{1}{2}AB = a\).
Suy ra \(MK = KN = NI = IM\).
Tứ giác \(KMIN\) có bốn cạnh bằng nhau nên là hình thoi.
Áp dụng tính chất về đường chéo vào hình thoi \(KMIN\) ta được: \(MN \bot KI;MN\) là đường phân giác \(\widehat {KMI}\).
Cho tứ giác ABCD có \(\widehat C = {50^ \circ },\widehat D = {80^ \circ }\), AD = BC. Gọi E, F lần lượt là trung điểm của các cạnh AB và CD. Tính số đo góc EFC.
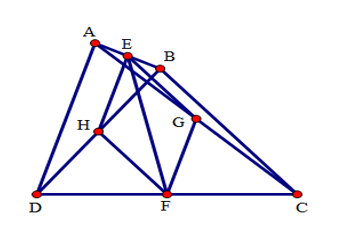
Gọi G, H lần lượt là trung điểm của AC, BD.
Vì E, G lần lượt là trung điểm của AB, AC nên EG là đường trung bình của tam giác ABC. Suy ra \(EG = \dfrac{1}{2}BC;\,\,EG//BC.\)
Chứng minh tương tự ta cũng có:
\(GF = \dfrac{1}{2}AD,FH = \dfrac{1}{2}BC,HE = \dfrac{1}{2}AD;\,\,GF//AD;\,\,FH//BC;\,\,HE//AD.\)
Mà AD = BC (gt), nên EG = GF = FH = HE.
Suy ra: tứ giác EGFH là thoi.
Suy ra EF là tia phân giác của góc \(\widehat {HFG} \Rightarrow \widehat {EFG} = \dfrac{1}{2}\widehat {HFG}.\)
\(\widehat {GFC} = \widehat {ADC} = {80^0}\,\left( {do\,\,GF//AD} \right);\,\,\widehat {HFD} = \widehat {BCD} = {50^0}\,\,\,\left( {do\,\,\,FH//BC} \right).\)
Do đó \(\widehat {HFG} = {180^0} - \left( {\widehat {GFC} + \widehat {HFD}} \right) = {50^0} \Rightarrow \widehat {EFG} = \dfrac{1}{2}{.50^0} = {25^0}\).
Vậy \(\widehat {EFC} = \widehat {EFG} + \widehat {GFC} = {25^0} + {80^0} = {105^0}\).
Hãy chọn câu sai.
+ Tứ giác có bốn cạnh bằng nhau là hình thoi.
+ Hình bình hành có hai cạnh kề bằng nhau là hình thoi.
+ Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi..
+ Hình bình hành có một đường chéo là đường phân giác của một góc là hình thoi.
Nên A, C, D đúng, B sai.
Hình thoi không có tính chất nào dưới đây?
Hình thoi có tất cả các tính chất của hình bình hành
+ Các cạnh đối song song và bằng nhau, các góc đối bằng nhau
+ Hai đường chéo giao nhau tại trung điểm mỗi đường.
Ngoài ra còn có
+ Hai đường chéo vuông góc với nhau.
+ Hai đường chéo là các đường phân giác của các góc của hình thoi.
Cho các hình sau, chọn khẳng định đúng.
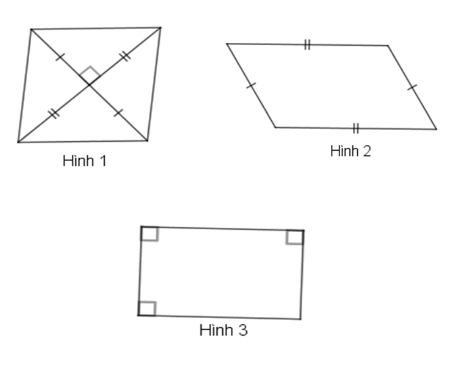
Hình 1 là hình thoi vì có hai đường chéo giao nhau tại trung điểm mỗi đường và vuông góc với nhau.
Hình 2 không là hình thoi vì bốn cạnh không bằng nhau.
Hình 3 không là hình thoi vì bốn cạnh không bằng nhau.
Hình thoi có chu vi bằng $20$$cm$ thì độ dài cạnh của nó bằng
Gọi cạnh của hình thoi là \(a\,\,cm\,\left( {a > 0} \right)\) .
Vì hình thoi có bốn cạnh bằng nhau nên chu vi hình thoi là \(4a = 20 \Leftrightarrow a = 5\,cm\) .
Vậy cạnh hình thoi có độ dài là \(5\,cm\) .

