Biểu thức nào sau đây được gọi là đơn thức.
Đơn thức là biểu thức đại số chỉ gồm một số hoặc một biến, hoặc một tích giữa các số và biến.
Tìm x sao cho \(f\left( x \right) - g\left( x \right) + h\left( x \right) = 0.\)
Ta có:
\(\begin{array}{l}f\left( x \right) - g\left( x \right) + h\left( x \right) = 0\\ \Leftrightarrow 2x + 1 = 0\\ \Leftrightarrow 2x\,\,\,\,\,\,\,\, = - 1\\ \Leftrightarrow \,\,\,\,x\,\,\,\,\,\,\,\, = \dfrac{{ - 1}}{2}\end{array}\).
Vậy \(x = \dfrac{{ - 1}}{2}.\)
Tính: \(f\left( x \right) - g\left( x \right) + h\left( x \right)\).
\(\begin{array}{l}\,f\left( x \right) = {x^3} - 2{x^2} + 3x + 1\\g\left( x \right) = {x^3} + x - 1\\h\left( x \right) = 2{x^2} - 1\\ \Rightarrow f\left( x \right) - g\left( x \right) + h\left( x \right)\\ = {x^3} - 2{x^2} + 3x + 1 - \left( {{x^3} + x - 1} \right) + \left( {2{x^2} - 1} \right)\\ = \,{x^3} - 2{x^2} + 3x + 1 - {x^3} - x + 1 + 2{x^2} - 1\\ = \left( {{x^3} - {x^3}} \right) + \left( { - 2{x^2} + 2{x^2}} \right) + \left( {3x - x} \right) + 1 + 1 - 1\\ = 2x + 1\end{array}\).
Vậy \(f\left( x \right) - g\left( x \right) + h\left( x \right) = 2x + 1.\)
Tính: \(f\left( x \right) - g\left( x \right) + h\left( x \right)\).
\(\begin{array}{l}\,f\left( x \right) = {x^3} - 2{x^2} + 3x + 1\\g\left( x \right) = {x^3} + x - 1\\h\left( x \right) = 2{x^2} - 1\\ \Rightarrow f\left( x \right) - g\left( x \right) + h\left( x \right)\\ = {x^3} - 2{x^2} + 3x + 1 - \left( {{x^3} + x - 1} \right) + \left( {2{x^2} - 1} \right)\\ = \,{x^3} - 2{x^2} + 3x + 1 - {x^3} - x + 1 + 2{x^2} - 1\\ = \left( {{x^3} - {x^3}} \right) + \left( { - 2{x^2} + 2{x^2}} \right) + \left( {3x - x} \right) + 1 + 1 - 1\\ = 2x + 1\end{array}\).
Vậy \(f\left( x \right) - g\left( x \right) + h\left( x \right) = 2x + 1.\)
Khi \(\widehat {xOy} = {60^0}\) thì ta có:
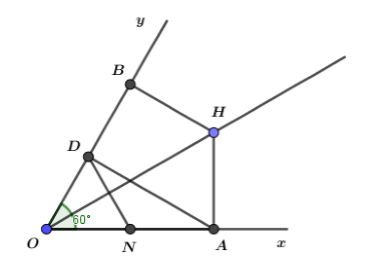
Gọi N là trung điểm của OA, khi đó trong tam giác vuông AOD (vuông tại D)
Khi đó \(D{\rm N} = O{\rm N} = \dfrac{{OA}}{2}\) (đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền)
\( \Rightarrow \Delta {\rm N}OD\) cân tại N (1)
Mặt khác \(\widehat {AOD} = \widehat {xOy} = {60^0}\) (2)
Từ (1) và (2), suy ra \(\Delta {\rm N}OD\) là tam giác đều.
\( \Rightarrow OD = O{\rm N}\) mà \(O{\rm N} = \dfrac{1}{2}OA\)
\( \Rightarrow OD = \dfrac{1}{2}OA\,\,hay\,\,OA = 2OD\).
Chọn câu đúng.
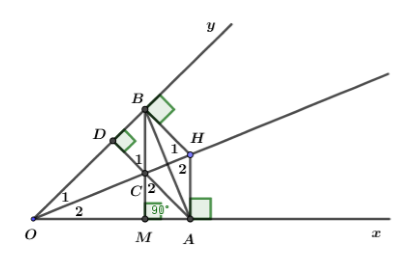
Xét hai tam giác vuông \(HBO\) và \(HAO\) ta có:
Cạnh huyền \(OH\,chung\)
Góc nhọn \({O_1} = {O_2}\)
\( \Rightarrow \Delta HBO = \Delta HAO\,\) (cạnh huyền-góc nhọn)
Do đó: \(OA = OB\) (cạnh tương ứng)
Xét tam giác \(OAB\) cân tại O do \(OA = OB\) (cmt)
Mà \(AD \bot BO\) \( \Rightarrow AD\) là đường cao.
C nằm trên tia phân giác góc O. Hay OC là đường phân giác góc O.
Trong một tam giác cân đường phân giác cũng chính là đường cao.
Mặt khác CO giao với AD tại C.
\( \Rightarrow C\) là trực tâm của tam giác OAB.
Do đó BC là đường cao.
Hay \(BC \bot OA\) hay \(BC \bot {\rm{Ox}}\)
Tam giác \(HAB\) là tam giác:
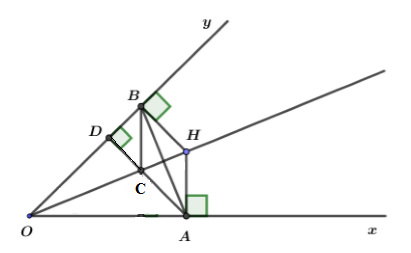
Vì \(H\) nằm trên tia phân giác của góc \(xOy\)
mà \(HA \,\bot \,{\rm{Ox,}}\,{\rm{HB}} \,\bot \,{\rm{Oy}}\) nên ta có:
\(HA = HB\) (tính chất các điểm thuộc tia phân giác)
\( \Rightarrow \Delta HAB\) cân tại \(H\).
Tam giác \(HAB\) là tam giác:

Vì \(H\) nằm trên tia phân giác của góc \(xOy\)
mà \(HA \,\bot \,{\rm{Ox,}}\,{\rm{HB}} \,\bot \,{\rm{Oy}}\) nên ta có:
\(HA = HB\) (tính chất các điểm thuộc tia phân giác)
\( \Rightarrow \Delta HAB\) cân tại \(H\).
Đơn thức nào sau đây đồng dạng với đơn thức \( - \dfrac{2}{3}x{y^2}\).
Ta có: \(3xy\left( { - 2y} \right) = - 6x{y^2}\) có cùng phần biến với \( - \dfrac{2}{3}x{y^2}\).
Vậy hai đơn thức đó đồng dạng với nhau.
Bậc của đa thức \(M = {x^6} + 5{x^2}{y^2} + {y^4} - {x^4}{y^3} - 25\) là:
Ta có: \(M = {x^6} + 5{x^2}{y^2} + {y^4} - {x^4}{y^3} - 25\)
Đa thức này đã là đa thức thu gọn.
Trong đa thức: \(M = {x^6} + 5{x^2}{y^2} + {y^4} - {x^4}{y^3} - 25\).
Hạng tử: \({x^6}\) có bậc 6. Hạng tử: \({x^2}{y^2}\) có bậc 4. Hạng tử \({y^4}\) có bậc 4. Hạng tử \( - {x^4}{y^3}\) có bậc 7. Hạng tử \( - 25\) có bậc 0.
Bậc cao nhất trong các bậc đó là 7.
\( \Rightarrow M\) có bậc là 7.
Trong tam giác \(M{\rm N}P\) có điểm \(O\) cách đều 3 đỉnh tam giác. Khi đó O là giao điểm của:
Vì O cách đều 3 đỉnh của tam giác nên O là giao điểm của ba đường trung trực.
Cách sắp xếp nào của đa thức sau đây theo lũy thừa giảm dần của biến x là đúng?
Ta thấy cách sắp xếp theo lũy thừa giảm dần của biến x là: \(4{x^5} - 3{x^4} + 5{x^3} - {x^2} + 2x + 1\).
Giá trị của biểu thức \(5{x^2}y + 10{y^2}x\) tại \(x = - 2\) và \(y = - 1\) là:
Thay các giá trị \(x = - 2\) và \(y = - 1\) vào biểu thức \(5{x^2}y + 10{y^2}x\) ta được:
\(\begin{array}{l}5{x^2}y + 10{y^2}x = 5. {\left( { - 2} \right)^2}. \left( { - 1} \right) + 10. {\left( { - 1} \right)^2}. \left( { - 2} \right)\\ = 5. 4. \left( { - 1} \right) + 10. 1. \left( { - 2} \right)\\ = - 20 - 20 = - 40\end{array}\).
Số nào sau đây là nghiệm của đa thức \(g\left( y \right) = \dfrac{2}{3}y + 2\).
Ta có: \(g\left( y \right) = 0 \Leftrightarrow \dfrac{2}{3}y + 2 = 0\) \( \Leftrightarrow \dfrac{2}{3}y = - 2 \Leftrightarrow y = - 3\).
Vậy \(y = - 3\) là nghiệm của đa thức \(g\left( y \right) = \dfrac{2}{3}y + 2\).
Cho hình vẽ, ta có MN là đường trung trực của đoạn thẳng AB và \(MI > {\rm N}I\). Khi đó ta có:
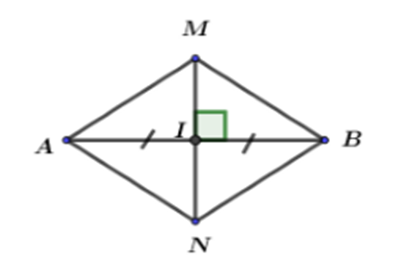
Ta có: MN là đường trung trực của đoạn thẳng AB và \(MI > {\rm N}I\)
Lại có AM có hình chiếu MI, NB có hình chiếu NI.
Mà: \(MI > {\rm N}I \Rightarrow AM > {\rm N}B\) (đường xiên có hình chiếu lớn hơn thì lớn hơn).
Tam giác \(ABC\) có các số đo như hình dưới, ta có:
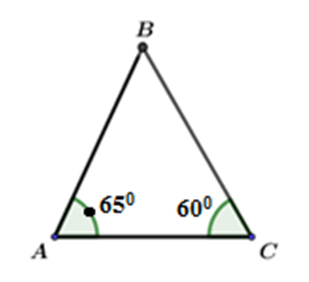
Xét tam giác \(ABC\), ta có:
\(\begin{array}{l}\widehat A + \widehat B + \widehat C = {180^0}\\ \Rightarrow \widehat B = {180^0} - \left( {\widehat A + \widehat C} \right)\\ = {180^0} - \left( {{{65}^0} + {{60}^0}} \right)\\ = {180^0} - {125^0}\\ = \,{55^0}\end{array}\)
\( \Rightarrow \widehat A > \widehat C > \widehat B \Rightarrow BC > AB > AC\) (trong một tam giác cạnh đối diện với góc lớn hơn là cạnh lớn hơn).
Bộ ba số đo nào sau đây có thể là độ dài ba cạnh của một tam giác vuông?
Ta có:
\(\begin{array}{l} + )\,\,{14^2} = 196 \ne {9^2} + {7^2}\\ + )\,\,{5^2} = 25\,\, \ne \,\,{2^2} + {3^2} = 13\\ + )\,\,{12^2} = 144 \ne {4^2} + {9^2} = 97\\ + )\,{10^2} = 100 = {6^2} + {8^2}\end{array}\).
Chỉ có bộ \(6cm,\,8cm,\,10cm\) thỏa mãn định lý Pi-ta-go đảo. Vậy bộ ba số này là độ dài 3 cạnh của một tam giác vuông.
Tam giác cân có góc ở đỉnh là \({80^o}\). Số đo góc ở đáy là:
Giả sử tam giác ABC cân tại A có: \(\widehat A = {80^o}\). Ta sẽ tìm số đo góc B hoặc góc C.
Áp dụng định lí tổng ba góc trong tam giác ta có: \(\widehat A + \widehat B + \widehat C = {180^o}\)
\( \Rightarrow \widehat B + \widehat C = {180^o} - \widehat A = {180^o} - {80^o} = {100^o}\)
Do tam giác ABC cân tại A nên \(\widehat B = \widehat C\). Từ đó suy ra: \(\widehat B = \widehat C = \dfrac{{\widehat B + \widehat C}}{2} = \dfrac{{{{100}^o}}}{2} = {50^o}\).
Vậy số đo góc ở đáy là \({50^o}\).
Cho hai đa thức: \(P\left( x \right) = 2{x^2} - 10\) và \(Q\left( x \right) = {x^2} + x + 5\). Hiệu \(P\left( x \right) - Q\left( x \right)\) bằng:
Ta có:
\(\begin{array}{l}P\left( x \right) - Q\left( x \right) = 2{x^2} - 10 - \left( {{x^2} + x + 5} \right)\\ = 2{x^2} - 10 - {x^2} - x - 5\\ = {x^2} - x - 15\end{array}\).
Cho \(\Delta MNP\) có \(\widehat M = {40^0}\), các đường phân giác \(NH\) và \(PK\) của \(\widehat N\) và \(\widehat P\) cắt nhau tại I. Khi đó \(\widehat {NIP}\) bằng:
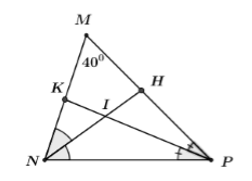
Xét \(\Delta MNP\) có: \(\widehat M + \widehat {MNP} + \widehat {MPN} = {180^0}\) (định lý tổng ba góc trong một tam giác)
\( \Rightarrow \widehat {MNP} + \widehat {MPN} = {180^0} - \widehat M = {180^0} - {40^0} = {140^0}\left( 1 \right)\)
Vì NH là phân giác của \(\widehat {MNP}\left( {gt} \right) \Rightarrow \widehat {HNP} = \dfrac{{\widehat {MNP}}}{2}\left( 2 \right)\) (tính chất tia phân giác)
Vì PK là phân giác của \(\widehat {MNP}\left( {gt} \right) \Rightarrow \widehat {NPK} = \dfrac{{\widehat {MPN}}}{2}\left( 3 \right)\) (tính chất tia phân giác)
Từ (1) (2) và (3) \( \Rightarrow \widehat {INP} + \widehat {IPN} = \dfrac{{\widehat {MNP}}}{2} + \dfrac{{\widehat {MPN}}}{2} = {140^0}:2 = {70^0}\) hay \(\widehat {INP} + \widehat {IPN} = {70^0}\left( * \right)\)
Xét \(\Delta INP\) có: \(\widehat {INP} + \widehat {IPN} + \widehat {NIP} = {180^0}\left( {**} \right)\)( định lý tổng ba góc trong một tam giác)
Từ (*) và (**) \( \Rightarrow \widehat {NIP} = {180^0} - \left( {\widehat {INP} + \widehat {IPN}} \right) = {180^0} - {70^0} = {110^0}\)

