Tứ giác

Tổng các góc trong 1 tứ giác bằng $360^\circ$.

Các góc của tứ giác có thể là 4 góc vuông vì khi đó tổng các góc của tứ giác này bằng $360^\circ$.

Các trường hợp còn lại không thỏa mãn định lí tổng các góc trong tam giác.

Tứ giác ABCD là hình gồm bốn đoạn thẳng AB, BC, CD, DA trong đó bất kì hai đoạn thẳng nào cũng không nằm trên cùng một đường thẳng.

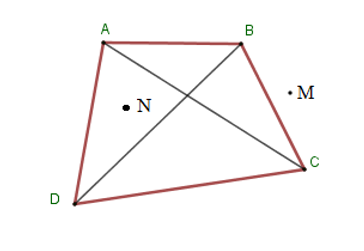
Từ hình vẽ ta thấy: Điểm $M$ nằm ngoài tứ giác $ABCD$ và điểm $N$ nằm trong tứ giác $ABCD$.

Trong tứ giác ABCD có:

$\widehat {\,C\,\,} + \widehat {\,D\,\,} = 360^\circ  - \left( {\widehat {A\,\,} + \widehat {\,B\,\,}} \right) = 360^\circ  - 140^\circ  = 220^\circ$.

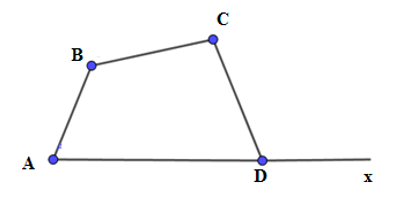
$\widehat {CDx}$ là góc ngoài đỉnh D.

Tứ giác ABCD có: $\widehat {D\,} = 360^\circ  - \left( {\widehat {A\,\,} + \widehat {B\,\,} + \widehat {C\,\,}} \right)$$= 360^\circ  - \left( {65^\circ  + 117^\circ  + 71^\circ } \right) = 107^\circ$

Vì  $\widehat {ADC}$  và  $\widehat {CDx}$  là hai góc kề bù nên $\widehat {CDx} = 180^\circ  - \widehat {D\,} = 180^\circ  - 107^\circ  = 73^\circ$.

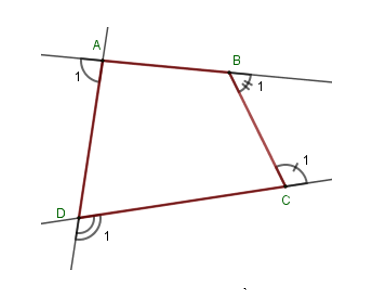
Gọi góc ngoài tại bốn đỉnh $A,B,\,C,\,D$ của tứ giác $ABCD$ lần lượt là $\widehat {{A_1}};\,\widehat {{B_1}};\,\widehat {{C_1}};\,\widehat {{D_1}}$. Khi đó ta có:

$\widehat A + \widehat {{A_1}} = 180^\circ  \Rightarrow \widehat {{A_1}} = 180^\circ  - \widehat A$; $\widehat B + \widehat {{B_1}} = 180^\circ  \Rightarrow \widehat {{B_1}} = 180^\circ  - \widehat B$; $\widehat C + \widehat {{C_1}} = 180^\circ  \Rightarrow \widehat {{C_1}} = 180^\circ  - \widehat C$ và $\widehat D + \widehat {{D_1}} = 180^\circ  \Rightarrow \widehat {{D_1}} = 180^\circ  - \widehat D$.

Suy ra: $\widehat {{A_1}} + \widehat {{B_1}} + \widehat {{C_1}} + \widehat {{D_1}}$$= 180^\circ  - \widehat A + 180^\circ  - \widehat B + 180^\circ  - \widehat C + 180^\circ  - \widehat D$ $= 720^\circ  - \left( {\widehat A + \widehat B + \widehat C + \widehat D} \right) = 720^\circ  - 360^\circ  = 360^\circ$

(Vì $\widehat A + \widehat B + \widehat C + \widehat D = 360^\circ$)

Vậy tổng số đo các góc ngoài tại $4$ đỉnh $A,B,\,C,\,D$ là $360^\circ$.

Mà tổng số đo góc ngoài tại hai đỉnh $B,C$ bằng $200^\circ$ nên tổng số đo góc ngoài tại hai đỉnh $A,D$ bằng $360^\circ  - 200^\circ  = 160^\circ$.

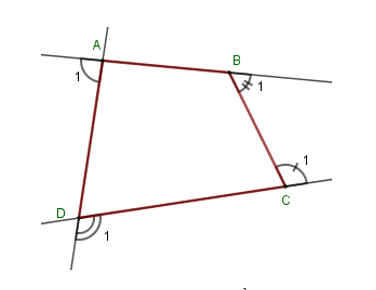
Gọi góc ngoài tại bốn đỉnh $A,B,\,C,\,D$ của tứ giác $ABCD$ lần lượt là $\widehat {{A_1}};\,\widehat {{B_1}};\,\widehat {{C_1}};\,\widehat {{D_1}}$. Khi đó ta có:

$\widehat A + \widehat {{A_1}} = 180^\circ$$\Rightarrow \widehat {{A_1}} = 180^\circ  - \widehat A$$= 180^\circ  - 80^\circ  = 100^\circ$.

Theo kết quả các câu trước ta có $\widehat {{A_1}} + \widehat {{B_1}} + \widehat {{C_1}} + \widehat {{D_1}} = 360^\circ$$\Rightarrow \widehat {{B_1}} + \widehat {{C_1}} + \widehat {{D_1}} = 360^\circ  - \widehat {{A_1}} = 360^\circ  - 100^\circ  = 260^\circ$.

Vậy $\widehat {{B_1}} + \widehat {{C_1}} + \widehat {{D_1}} = 260^\circ$.

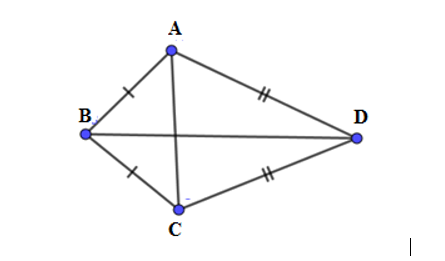
Xét tam giác $ABC$ có: $\widehat B = 100^\circ ;AB = BC \Rightarrow \Delta ABC$cân tại $B$  $\Rightarrow \widehat {BAC} = \widehat {BCA} = \dfrac{{180^\circ  - 100^\circ }}{2} = 40^\circ$.

Xét tam giác $ADC$ có $CD = DA \Rightarrow \Delta ADC$ cân tại $D$ có $\widehat {ADC} = 70^\circ$ nên $\widehat {DAC} = \widehat {DCA} = \dfrac{{180^\circ  - 70^\circ }}{2} = 55^\circ$.

Từ đó ta có: $\widehat A = \widehat {BAD} = \widehat {BAC} + \widehat {CAD} = 40^\circ  + 55^\circ  = 95^\circ$.

Và $\widehat C = \widehat {BCD} = \widehat {BCA} + \widehat {ACD} = 40^\circ  + 55^\circ  = 95^\circ$.

Nên $\widehat A = \widehat C = 95^\circ$.

Vì $\widehat {A\,\,}:\widehat {B\,\,}:\widehat {C\,\,}:\widehat {D\,\,} = 4:3:2:1$nên ta có:

$\dfrac{{\widehat A}}{4} = \dfrac{{\widehat B}}{3} = \dfrac{{\widehat C}}{2} = \dfrac{{\widehat D}}{1} = \dfrac{{\widehat A + \widehat B + \widehat C + \widehat D}}{{4 + 3 + 2 + 1}} = \dfrac{{\widehat A + \widehat B + \widehat C + \widehat D}}{{10}}$  (tính chất tỉ lệ thức).

Mà $\widehat A + \widehat B + \widehat C + \widehat D = 360^\circ$ nên ta có $\dfrac{{\widehat A}}{4} = \dfrac{{\widehat B}}{3} = \dfrac{{\widehat C}}{2} = \dfrac{{\widehat D}}{1} = \dfrac{{\widehat A + \widehat B + \widehat C + \widehat D}}{{10}} = \dfrac{{360^\circ }}{{10}} = 36^\circ$.

$\Rightarrow \widehat A = 4.36^\circ  = 144^\circ$ ; $\widehat B = 3.36^\circ  = 108^\circ ;\,\widehat C = 2.36^\circ  = 72^\circ ;\,\widehat D = 1.36^\circ  = 36^\circ$.

Nên số đo góc $\widehat A;\widehat B;\widehat C;\,\widehat D$ lần lượt là  $\widehat {A\,\,} = 144^\circ ;\,\,\widehat {B\,\,} = 108^\circ ;\,\,\widehat {C\,\,} = 72^\circ ;\,\,\widehat {D\,\,} = 36^\circ$.

Định lý: Tổng các góc của một tứ giác bằng ${360^0}$ nên C đúng, B sai.

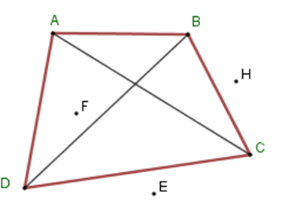
Từ hình vẽ ta thấy các điểm $E,\,H$ nằm bên ngoài tứ giác và điểm $F$ nằm bên trong tứ giác$ABCD$  nên D sai.

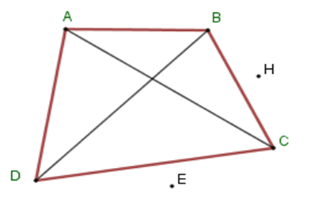
Tứ giác $ABCD$ có các cặp góc đối nhau là $\widehat A;\,\widehat C$ và $\widehat B;\,\widehat D$  còn $\widehat A;\,\widehat B$ là hai góc kề nhau nên C sai.

Xét tứ giác $ABCD$ có $\widehat A + \widehat B + \widehat C + \widehat D = 360^\circ$(định lý)

hay $60^\circ  + 135^\circ  + \widehat C + 29^\circ  = 360^\circ  \Rightarrow \widehat C = 360^\circ  - 60^\circ  - 135^\circ  - 29^\circ$ $\Leftrightarrow \widehat C = 136^\circ$ .

Xét tứ giác $ABCD$ có $\widehat A + \widehat B + \widehat C + \widehat D = 360^\circ$(định lý)

Hay $50^\circ  + \widehat B + 150^\circ  + 45^\circ  = 360^\circ  \Rightarrow \widehat B = 360^\circ  - 50^\circ  - 150^\circ  - 45^\circ$$\Leftrightarrow \widehat B = 115^\circ$

Nên góc ngoài tại đỉnh $B$ có số đo là $180^\circ  - \widehat B = 180^\circ  - 115^\circ  = 65^\circ$ .

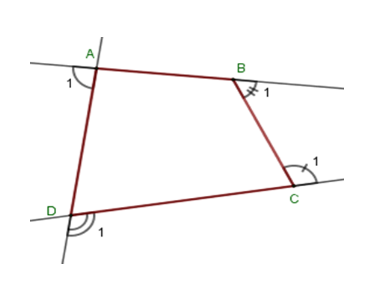
Gọi góc ngoài tại bốn đỉnh $A,B,\,C,\,D$ của tứ giác $ABCD$ lần lượt là $\widehat {{A_1}};\,\widehat {{B_1}};\,\widehat {{C_1}};\,\widehat {{D_1}}$ . Khi đó ta có

$\widehat A + \widehat {{A_1}} = 180^\circ  \Rightarrow \widehat {{A_1}} = 180^\circ  - \widehat A$; $\widehat B + \widehat {{B_1}} = 180^\circ  \Rightarrow \widehat {{B_1}} = 180^\circ  - \widehat B$; $\widehat C + \widehat {{C_1}} = 180^\circ  \Rightarrow \widehat {{C_1}} = 180^\circ  - \widehat C$ và $\widehat D + \widehat {{D_1}} = 180^\circ  \Rightarrow \widehat {{D_1}} = 180^\circ  - \widehat D$

Suy ra $\widehat {{A_1}} + \widehat {{B_1}} + \widehat {{C_1}} + \widehat {{D_1}} = 180^\circ  - \widehat A + 180^\circ  - \widehat B + 180^\circ  - \widehat C + 180^\circ  - \widehat D$ $= 720^\circ  - \left( {\widehat A + \widehat B + \widehat C + \widehat D} \right) = 720^\circ  - 360^\circ  = 360^\circ$

(Vì $\widehat A + \widehat B + \widehat C + \widehat D = 360^\circ$)

Vậy tổng số đo các góc ngoài tại $4$ đỉnh $A,B,\,C,\,D$ là $360^\circ$ .

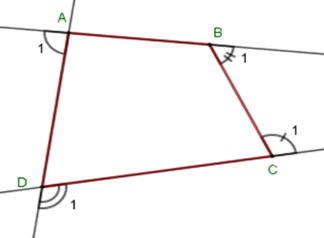
Gọi góc ngoài tại bốn đỉnh $A,B,\,C,\,D$ của tứ giác $ABCD$ lần lượt là $\widehat {{A_1}};\,\widehat {{B_1}};\,\widehat {{C_1}};\,\widehat {{D_1}}$ . Khi đó ta có

$\widehat A + \widehat {{A_1}} = 180^\circ  \Rightarrow \widehat {{A_1}} = 180^\circ  - \widehat A = 180^\circ  - 100^\circ  = 80^\circ .$

Theo kết quả các câu trước ta có $\widehat {{A_1}} + \widehat {{B_1}} + \widehat {{C_1}} + \widehat {{D_1}} = 360^\circ$$\Rightarrow \widehat {{B_1}} + \widehat {{C_1}} + \widehat {{D_1}} = 360^\circ  - \widehat {{A_1}} = 360^\circ  - 80^\circ  = 280^\circ$ .

Vậy $\widehat {{B_1}} + \widehat {{C_1}} + \widehat {{D_1}} = 280^\circ$.

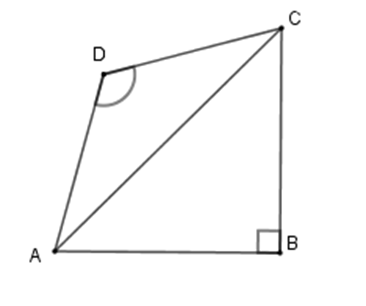
Xét tam giác $ABC$ có $\widehat B = 90^\circ ;AB = BC \Rightarrow \Delta ABC$ vuông cân $\Rightarrow \widehat {BAC} = \widehat {BCA} = \dfrac{{90^\circ }}{2} = 45^\circ$

Xét tam giác $ADC$ có $CD = DA \Rightarrow \Delta ADC$ cân tại $D$ có $\widehat {ADC} = 120^\circ$ nên $\widehat {DAC} = \widehat {DCA} = \dfrac{{180^\circ  - 120^\circ }}{2} = 30^\circ$

Từ đó ta có $\widehat A = \widehat {BAD} = \widehat {BAC} + \widehat {CAD} = 45^\circ  + 30^\circ  = 75^\circ$

Và $\widehat C = \widehat {BCD} = \widehat {BCA} + \widehat {ACD} = 45^\circ  + 30^\circ  = 75^\circ$

Nên $\widehat A = \widehat C = 75^\circ$ .

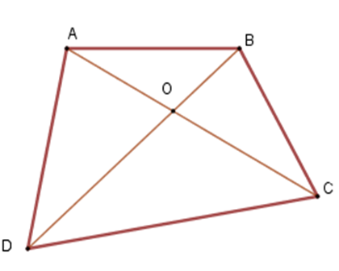
+ Xét tam giác $OAB$ ta có $OA + OB > AB$(vì trong một tam giác, tổng độ dài hai cạnh bất kì bao giờ cũng lớn hơn độ dài cạnh còn lại) .

Tương tự ta có $OC + OD > CD;\,OB + OC > BC;\,OA + OD > AD$

Cộng vế với vế ta được $OA + OB + OC + OD + OB + OC + OA + OD > AB + BC + CD + AD$

$\Leftrightarrow 2\left( {OA + OB + OC + OD} \right) > AB + BC + CD + DA$ $\Leftrightarrow OA + OB + OC +OD> \dfrac{{AB + BC + CD + DA}}{2}$  nên B đúng.

+ Xét tam giác $ABC$ ta có $AB + BC > AC$ (vì trong một tam giác, tổng độ dài hai cạnh bất kì bao giờ cũng lớn hơn độ dài cạnh còn lại) .

Tương tự ta có $BC + CD > BD;\,CD + DA > AC;\,AD + DB > BD$

Cộng vế với vế ta được: $AB + BC + BC + CD + CD + DA + DA + AB > AC + BD + AC + BD$

$\Leftrightarrow 2\left( {AB + BC + CD + DA} \right) > 2\left( {AC + BD} \right)$ $\Leftrightarrow AB + BC + CD + DA > AC + BD$ mà $AC + BD = OA + OC + OB + OD$ nên $AB + BC + CD + DA > OA + OB + OC + OD$ nên A đúng.

Vậy cả A, B đều đúng.

Vì số đo của các góc $\widehat A;\,\widehat B;\,\widehat C;\,\widehat D$  tỉ lệ thuận với $4;3;5;6$ nên ta có

$\dfrac{{\widehat A}}{4} = \dfrac{{\widehat B}}{3} = \dfrac{{\widehat C}}{5} = \dfrac{{\widehat D}}{6} = \dfrac{{\widehat A + \widehat B + \widehat C + \widehat D}}{{4 + 3 + 5 + 6}} = \dfrac{{\widehat A + \widehat B + \widehat C + \widehat D}}{{18}}$  (tính chất dãy tỉ số bằng nhau)

Mà $\widehat A + \widehat B + \widehat C + \widehat D = 360^\circ$ nên ta có $\dfrac{{\widehat A}}{4} = \dfrac{{\widehat B}}{3} = \dfrac{{\widehat C}}{5} = \dfrac{{\widehat D}}{6} = \dfrac{{\widehat A + \widehat B + \widehat C + \widehat D}}{{18}} = \dfrac{{360^\circ }}{{18}} = 20^\circ$

$\Rightarrow \widehat A = 4.20^\circ  = 80^\circ$ ; $\widehat B = 3.20^\circ  = 60^\circ ;\,\widehat C = 5.20^\circ  = 100^\circ ;\,\widehat D = 6.20^\circ  = 120^\circ$

Nên số đo góc $\widehat A;\widehat B;\widehat C;\,\widehat D$ lần lượt là $80^\circ ;\,60^\circ ;\,100^\circ ;\,120^\circ$ .

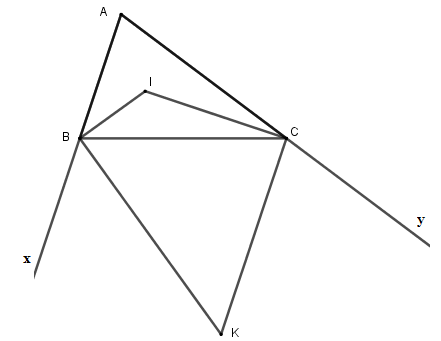
Xét tam giác $ABC$ có: $\widehat A + \widehat {ABC} + \widehat {BCA} = 180^\circ  \Leftrightarrow \widehat {ABC} + \widehat {BCA} = 120^\circ$.

Vì $BI$ là phân giác $\widehat {BAC} \Rightarrow \widehat {CBI} = \dfrac{1}{2}\widehat {BAC}$.

Vì $CI$ là phân giác $\widehat {BCA} \Rightarrow \widehat {BCI} = \dfrac{1}{2}\widehat {BCA}$.

Từ đó: $\widehat {CBI} + \widehat {BCI} = \dfrac{1}{2}\left( {\widehat {BAC} + \widehat {BCA}} \right) = \dfrac{1}{2}.120^\circ  = 60^\circ$.

Xét tam giác $BCI$ có: $\widehat {BCI} + \widehat {BIC} + \widehat {CBI} = 180^\circ$ nên $\widehat {BIC} = 180^\circ  - \left( {\widehat {BCI} + \widehat {CBI}} \right) = 180^\circ  - 60^\circ  = 120^\circ$.

Vì $BI$ là phân giác $\widehat {BAC} \Rightarrow \widehat {CBI} = \dfrac{1}{2}\widehat {BAC}$.

Vì $BK$ là phân giác $\widehat {CBx} \Rightarrow \widehat {CKB} = \dfrac{1}{2}\widehat {CBx}$.

Suy ra: $\widehat {CBK} + \widehat {CBI} = \dfrac{1}{2}\left( {\widehat {CBx} + \widehat {ABC}} \right) = \dfrac{1}{2}.180^\circ  = 90^\circ$  hay $\widehat {IBK} = 90^\circ$.

Tương tự ta có: $\widehat {ICK} = 90^\circ$.

Xét tứ giác $BICK$ có: $\widehat {BIC} + \widehat {IBC} + \widehat {ICK} + \widehat {BKC} = 360^\circ$$\Leftrightarrow \widehat {BKC} = 360^\circ  - 90^\circ  - 90^\circ  - 120^\circ  = 60^\circ$.

Vậy $\widehat {BIC} = 120^\circ ;\,\widehat {BKC} = 60^\circ .$