Tam giác \(ABC\) có \(\widehat A = 60^\circ \), các tia phân giác của góc \(B\) và \(C\) cắt nhau tại \(I.\) Các tia phân giác góc ngoài tại đỉnh \(B\) và \(C\) cắt nhau tại \(K\). Tính các góc \(\widehat {BIC};\,\widehat {BKC}.\)

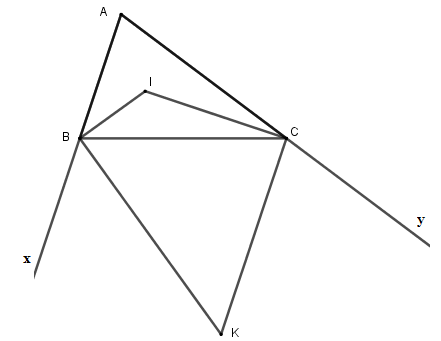
Xét tam giác \(ABC\) có: \(\widehat A + \widehat {ABC} + \widehat {BCA} = 180^\circ  \Leftrightarrow \widehat {ABC} + \widehat {BCA} = 120^\circ \).

Vì \(BI\) là phân giác \(\widehat {BAC} \Rightarrow \widehat {CBI} = \dfrac{1}{2}\widehat {BAC}\).

Vì \(CI\) là phân giác \(\widehat {BCA} \Rightarrow \widehat {BCI} = \dfrac{1}{2}\widehat {BCA}\).

Từ đó: \(\widehat {CBI} + \widehat {BCI} = \dfrac{1}{2}\left( {\widehat {BAC} + \widehat {BCA}} \right) = \dfrac{1}{2}.120^\circ  = 60^\circ \).

Xét tam giác \(BCI\) có: \(\widehat {BCI} + \widehat {BIC} + \widehat {CBI} = 180^\circ \) nên \(\widehat {BIC} = 180^\circ  - \left( {\widehat {BCI} + \widehat {CBI}} \right) = 180^\circ  - 60^\circ  = 120^\circ \).

Vì \(BI\) là phân giác \(\widehat {BAC} \Rightarrow \widehat {CBI} = \dfrac{1}{2}\widehat {BAC}\).

Vì \(BK\) là phân giác \(\widehat {CBx} \Rightarrow \widehat {CKB} = \dfrac{1}{2}\widehat {CBx}\).

Suy ra: \(\widehat {CBK} + \widehat {CBI} = \dfrac{1}{2}\left( {\widehat {CBx} + \widehat {ABC}} \right) = \dfrac{1}{2}.180^\circ  = 90^\circ \)  hay \(\widehat {IBK} = 90^\circ \).

Tương tự ta có: \(\widehat {ICK} = 90^\circ \).

Xét tứ giác \(BICK\) có: \(\widehat {BIC} + \widehat {IBC} + \widehat {ICK} + \widehat {BKC} = 360^\circ \)\( \Leftrightarrow \widehat {BKC} = 360^\circ  - 90^\circ  - 90^\circ  - 120^\circ  = 60^\circ \).

Vậy \(\widehat {BIC} = 120^\circ ;\,\widehat {BKC} = 60^\circ .\)