Tính số đo góc \(BDC\) , biết $\widehat {BAC} = 50^\circ $.
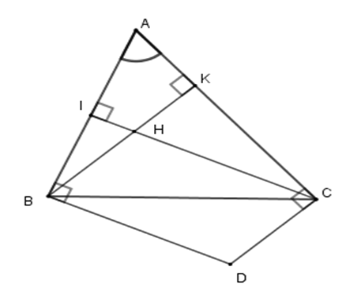
Xét tứ giác \(AIHK\) có \(\widehat A + \widehat {AIH} + \widehat {IHK} + \widehat {AKH} = 360^\circ \) (định lý tổng các góc trong tứ giác)
\( \Rightarrow \widehat {AHK} = 360^\circ - 50^\circ - 90^\circ - 90^\circ = 130^\circ \) .
Suy ra \(\widehat {BHC} = \widehat {IHK} = 130^\circ \) (hai góc đối đỉnh)
Vì tứ giác \(BHCD\) là hình bình hành nên $\widehat {BDC} = \widehat {BHC} = 130^\circ $ (tính chất).
Vậy \(\widehat {BDC} = 130^\circ \) .
Chọn câu trả lời đúng nhất. Tứ giác $BDCH$ là hình gì?
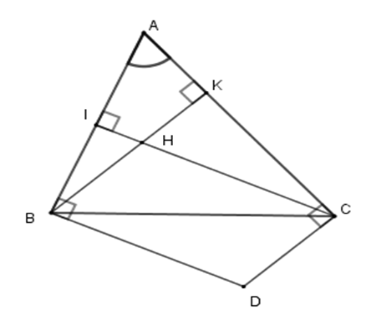
Gọi \(BK;\,CI\) là các đường cao của tam giác \(ABC\) . Khi đó \(BK \bot AC;\,CI \bot AB\) hay \(BH \bot AC;\,CH \bot AB\) (vì \(H\) là trực tâm).
Lại có \(BD \bot AB;\,CD \bot AC\) (giả thiết) nên $BD{\rm{//}}CH$ (cùng vuông với \(AB\) ) và $CD{\rm{//}}BH$ (cùng vuông với \(AC\) )
Suy ra tứ giác \(BHCD\) là hình bình hành (dhnb).
Chọn câu trả lời đúng nhất. Tứ giác $BDCH$ là hình gì?

Gọi \(BK;\,CI\) là các đường cao của tam giác \(ABC\) . Khi đó \(BK \bot AC;\,CI \bot AB\) hay \(BH \bot AC;\,CH \bot AB\) (vì \(H\) là trực tâm).
Lại có \(BD \bot AB;\,CD \bot AC\) (giả thiết) nên $BD{\rm{//}}CH$ (cùng vuông với \(AB\) ) và $CD{\rm{//}}BH$ (cùng vuông với \(AC\) )
Suy ra tứ giác \(BHCD\) là hình bình hành (dhnb).
Chọn câu trả lời đúng nhất. Tứ giác $BDCH$ là hình gì?

Gọi \(BK;\,CI\) là các đường cao của tam giác \(ABC\) . Khi đó \(BK \bot AC;\,CI \bot AB\) hay \(BH \bot AC;\,CH \bot AB\) (vì \(H\) là trực tâm).
Lại có \(BD \bot AB;\,CD \bot AC\) (giả thiết) nên $BD{\rm{//}}CH$ (cùng vuông với \(AB\) ) và $CD{\rm{//}}BH$ (cùng vuông với \(AC\) )
Suy ra tứ giác \(BHCD\) là hình bình hành (dhnb).
Chọn câu sai. Cho \(ABCD\) là hình bình hành. Khi đó:
Trong hình bình hành:
+ Hình bình hành có các cạnh đối song song.
+ Các cạnh đối bằng nhau.
+ Các góc đối bằng nhau.
+ Hai đường chéo cắt nhau tại trung điểm của mỗi đường nên D sai.
Điền cụm từ thích hợp vào chỗ trống: “Tứ giác có hai đường chéo… thì tứ giác đó là hình bình hành”.
Dấu hiệu nhận biết:
Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành.
Hãy chọn câu đúng. Tứ giác \(ABCD\) là hình bình hành nếu:
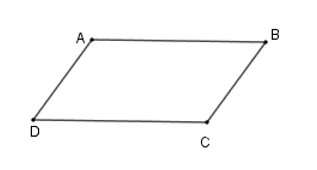
Tứ giác \(ABCD\) là hình bình hành khi \(AB = CD;AD = BC\).
Hãy chọn câu đúng. Cho hình bình hành \(ABCD\), gọi \(E\) là trung điểm của \(AB,{\rm{ }}F\) là trung điểm của \(CD.\) Khi đó:
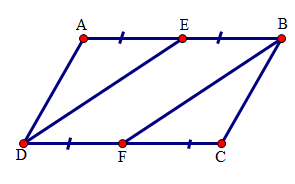
+ Vì \(ABCD\) là hình bình hành nên \(AB{\rm{//}}CD\); \(AB = CD\).
+ Xét tứ giác \(BEDF\) có \(BE = FD;\,BE{\rm{//}}FD\) (do \(AB{\rm{//}}CD\)) nên \(BEDF\) là hình bình hành.
Từ đó: \(DE = BF\) (tính chất hình bình hành).
Cho hình bình hành \(ABCD\) có \(\widehat A = 2\widehat B\). Số đo các góc của hình bình hành là:
Trong hình bình hành \(ABCD\) có: \(\widehat A = \widehat C,\widehat B = \widehat D\) (tính chất), \(\widehat A = 2\widehat B\).
Theo định lí tổng các góc trong tứ giác ta có:
\(\widehat A + \widehat B + \widehat C + \widehat D = 360^\circ \Rightarrow 2\left( {\widehat A + \widehat B} \right) = 360^\circ \Rightarrow \widehat A + \widehat B = 180^\circ \)
\( \Rightarrow 2\widehat B + \widehat B = 180^\circ \Rightarrow 3\widehat B = 180^\circ \Leftrightarrow \widehat B = 60^\circ \)
\( \Rightarrow \widehat A = 2\widehat B = 2.60^\circ = 120^\circ \)
Vậy \(\widehat A = \widehat C = 120^\circ ;\widehat B = \widehat D = 60^\circ \).
Tính số đo các góc của hình bình hành \(ABCD\) biết \(\widehat D - \widehat C = {40^0}\). Ta được:
Trong hình bình hành \(ABCD\) có: \(\widehat A = \widehat C,\widehat B = \widehat D\) (tính chất), \(\widehat D - \widehat C = {40^0} \Rightarrow \widehat D = \widehat C + 40^\circ \) nên \(\widehat B = \widehat D = \widehat C + 40^\circ \).
Theo định lí tổng các góc trong tứ giác ta có:
\(\widehat A + \widehat B + \widehat C + \widehat D = 360^\circ\)\( \Rightarrow 2\left( {\widehat C + \widehat D} \right) = 360^\circ \Rightarrow \widehat C + \widehat D = 180^\circ \)\( \Leftrightarrow \widehat C + \widehat C + 40^\circ = 180^\circ \Rightarrow 2\widehat C = 140^\circ \) \( \Leftrightarrow \widehat C = 70^\circ \)
\( \Rightarrow \widehat D = \widehat C + 40^\circ = 70^\circ + 40^\circ = 110^\circ \).
Do đó \(\widehat A = \widehat C = {70^0}\,\& \,\,\widehat B = \widehat D = {110^0}\).
Cho hình bình hành \(ABCD\). Tia phân giác của góc \(A\) cắt \(CD\) tại \(M\). Tia phân giác góc \(C\) cắt \(AB\) tại \(N\) (hình vẽ). Hãy chọn câu trả lời sai.
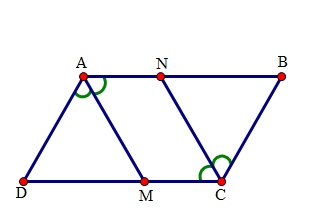
Vì \(\widehat {NAM} = \dfrac{1}{2}\widehat A,\widehat {MCN} = \dfrac{1}{2}\widehat C\) mà \(\widehat A = \widehat C\) (góc đối hình bình hành) nên \(\widehat {NAM} = \widehat {MCN}\).
Lại có: \(\widehat {BNC} = \widehat {MCN}\) (so le trong, \(AB\parallel CD\)).
Suy ra \(\widehat {NAM} = \widehat {BNC}\).
Mà hai góc \(\widehat {NAM},\widehat {BNC}\) ở vị trí đồng vị nên \(AM\parallel CN\).
Do \(AB\parallel CD(gt),N \in AB,M \in BC \Rightarrow AN\parallel MC\).
Tứ giác \(AMCN\) có \(AN\parallel CM,AM\parallel CN(cmt)\) nên là hình bình hành (dấu hiệu nhận biết).
Vì \(AMCN\) là hình bình hành nên \(AN = CM\) (tính chất) nên A, D đúng.
Vì \(MC//AB \Rightarrow AMCB\) là hình thang nên B đúng.
Vì \(AN//CD \Rightarrow ANCD\) là hình thang.
Chưa đủ điều kiện để \(ANCD\) là hình thang cân nên C sai.
Tính số đo góc \(BDC\), biết \(\widehat {BAC} = 40^\circ \).
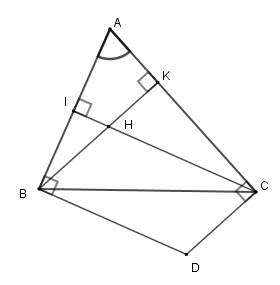
Xét tứ giác \(AIHK\) có \(\widehat A + \widehat {AIH} + \widehat {IHK} + \widehat {AKH} = 360^\circ \) (định lý tổng các góc trong tứ giác).
\( \Rightarrow \widehat {AHK} = 360^\circ - 40^\circ - 90^\circ - 90^\circ = 140^\circ \).
Suy ra \(\widehat {BHC} = \widehat {IHK} = 140^\circ \) (hai góc đối đỉnh).
Vì tứ giác \(BHCD\) là hình bình hành (theo câu trước) nên \(\widehat {BDC} = \widehat {BHC} = 140^\circ \) (tính chất).
Vậy \(\widehat {BDC} = 140^\circ \).
Chọn câu sai.
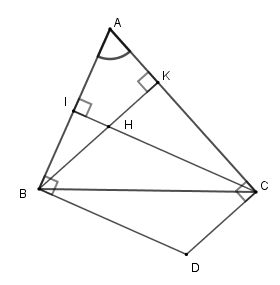
Gọi \(BK;\,CI\) là các đường cao của tam giác \(ABC\). Khi đó \(BK \bot AC;\,CI \bot AB\) hay \(BH \bot AC;\,CH \bot AB\) (vì \(H\) là trực tâm).
Lại có: \(BD \bot AB;\,CD \bot AC\) (giả thiết) nên \(BD{\rm{//}}CH\) (cùng vuông với \(AB\) ) và \(CD{\rm{//}}BH\) (cùng vuông với \(AC\))
Suy ra tứ giác \(BHCD\) là hình bình hành (dhnb).
Từ đó \(HB = CD;\,CH = BD\) nên D sai (ta chưa đủ điều kiện để chỉ ra được \(HB = HC\)).
Chọn câu sai.

Gọi \(BK;\,CI\) là các đường cao của tam giác \(ABC\). Khi đó \(BK \bot AC;\,CI \bot AB\) hay \(BH \bot AC;\,CH \bot AB\) (vì \(H\) là trực tâm).
Lại có: \(BD \bot AB;\,CD \bot AC\) (giả thiết) nên \(BD{\rm{//}}CH\) (cùng vuông với \(AB\) ) và \(CD{\rm{//}}BH\) (cùng vuông với \(AC\))
Suy ra tứ giác \(BHCD\) là hình bình hành (dhnb).
Từ đó \(HB = CD;\,CH = BD\) nên D sai (ta chưa đủ điều kiện để chỉ ra được \(HB = HC\)).
Cho tứ giác \(ABCD\). Gọi \(E\), \(F\) lần lượt là trung điểm của \(AB\) và \(CD.\)\(M,N,P,Q\) lần lượt là trung điểm của \(AF,CE,BF,DE\). Khi đó \(MNPQ\) là hình gì? Chọn đáp án đúng nhất.
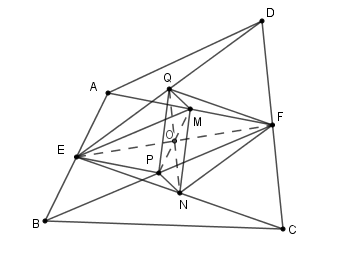
Nối \(EF;EP,FQ,EM,PM,QN\). Gọi \(O\) là giao của \(QN\) và \(EF\).
Xét tam giác \(CED\) có \(FN\) là đường trung bình nên \(\left\{ \begin{array}{l}FN = \dfrac{1}{2}DE = EQ\\FN//ED\end{array} \right. \Rightarrow NFQE\) là hình bình hành nên hai đường chéo \(QN\) và \(EF\) giao nhau tại trung điểm của mỗi đường. Suy ra \(O\) là trung điểm của \(QN\) (1) và \(EF\).
Xét tam giác \(ABF\) có \(EM\) là đường trung bình nên \(\left\{ \begin{array}{l}EM = \dfrac{1}{2}BF = PF\\EM//PF\end{array} \right. \Rightarrow EMFB\) là hình bình hành nên hai đường chéo \(PM\) và \(EF\) giao nhau tại trung điểm của mỗi đường. Mà \(O\) là trung điểm của \(EF\) nên \(O\) cũng là trung điểm của \(PM\) (2)
Từ (1) và (2) suy ra: tứ giác \(QMNP\) có hai đường chéo \(QN,PM\) giao nhau tại trung điểm \(O\) mỗi đường nên \(QMNP\) là hình bình hành (dhnb).
Cho hình bình hành \(ABCD\). Gọi \(E,F\) theo thứ tự là trung điểm của \(AD,{\rm{ }}BC\). Đường chéo \(AC\) cắt \(BE,DF\) theo thứ tự ở \(K,I{\rm{ }}\). Chọn khẳng định đúng nhất.
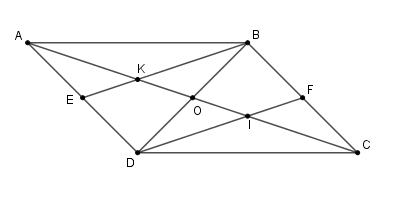
Gọi \(O\) là giao điểm của \(AC,BD\).
Vì \(ABCD\) là hình bình hành nên \(AC,BD\) giao nhau tại trung điểm \(O\) mỗi đường, hay \(AO = CO = \dfrac{{AC}}{2}\).
Xét tam giác \(ABD\) có \(BE,AO\) là hai đường trung tuyến cắt nhau tại \(K\) nên \(K\) là trọng tâm \(\Delta ABD\).
Suy ra \(AK = \dfrac{2}{3}AO = \dfrac{2}{3}.\dfrac{1}{2}AC = \dfrac{1}{3}AC\) (1)
Xét tam giác \(CBD\) có \(DF,CO\) là hai đường trung tuyến cắt nhau tại \(I\) nên \(I\) là trọng tâm \(\Delta CBD\).
Suy ra \(CI = \dfrac{2}{3}CO = \dfrac{2}{3}.\dfrac{1}{2}AC = \dfrac{1}{3}AC\) (2)
Lại có: \(AK + KI + CI = AC \Rightarrow KI = AC - AK - CI\) \( = AC - \dfrac{1}{3}AC - \dfrac{1}{3}AC = \dfrac{1}{3}AC\) (3)
Từ (1), 2) và (3) suy ra: \(AK = KI = IC\).
Hãy chọn câu sai:
Dấu hiệu nhận biết:
+ Tứ giác có các cạnh đối song song là hình bình hành nên A đúng.
+ Tứ giác có các cạnh đối bằng nhau là hình bình hành nên C đúng.
+ Tứ giác có các góc đối bằng nhau là hình bình hành nên D đúng.
Nhận thấy hình thang có hai góc kề một đáy bằng nhau là hình thang cân nên B sai.
Hãy chọn câu đúng. Tứ giác $ABCD$ là hình bình hành nếu.
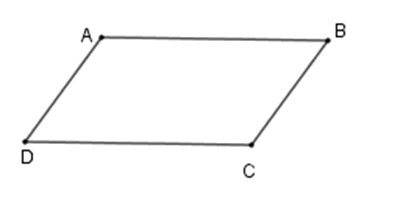
+ Tứ giác \(ABCD\) là hình bình hành khi $AB$ //$CD$ ,$BC{\rm{//}}AD$ nên C sai.
+ Tứ giác \(ABCD\) là hình bình hành khi $\widehat A = \widehat C;\widehat B = \widehat D$ nên D đúng.
+ A, B sai vì chưa đủ điều kiện để kết luận.
Hãy chọn câu đúng. Cho hình bình hành $ABCD$ có các điều kiện như hình vẽ, trong hình có:
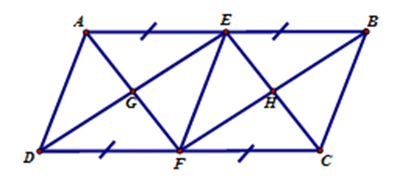
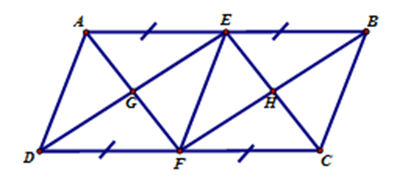
+ Vì \(ABCD\) là hình bình hành nên \(AB{\rm{//}}CD\); \(AD{\rm{//}}BC\) .
+ Xét tứ giác \(AEFD\) có \(AE = FD;\,AE{\rm{//}}FD\) (do \(AB{\rm{//}}CD\)) nên \(AEFD\) là hình bình hành.
+ Xét tứ giác \(BEFC\) có \(BE = FC;\,BE{\rm{//}}FC\) (do \(AB{\rm{//}}CD\)) nên \(BEFC\) là hình bình hành.
+ Xét tứ giác \(AECF\) có \(AE = FC;\,AE{\rm{//}}FC\) (do \(AB{\rm{//}}CD\)) nên \(AECF\) là hình bình hành.
+ Xét tứ giác \(BEDF\) có \(BE = FD;\,BE{\rm{//}}FD\) (do \(AB{\rm{//}}CD\)) nên \(BEDF\) là hình bình hành.
+ Vì \(AECF\) là hình bình hành nên \(AF{\rm{//}}EC \Rightarrow EH{\rm{//}}GF\) ; vì \(BEDF\) là hình bình hành nên \(ED{\rm{//}}BF \Rightarrow EG{\rm{//}}HF\)
Suy ra \(EGHF\) là hình bình hành.
Vậy có tất cả \(6\) hình bình hành: \(ABCD\); \(AEFD\); \(BEFC\); \(AECF\); \(BEDF\); \(EGHF\).
Cho hình bình hành $ABCD$ có \(\widehat A = 3\widehat B\) . Số đo các góc của hình bình hành là:
Trong hình bình hành $ABCD$ có: \(\widehat A = \widehat C,\widehat B = \widehat D\) (tính chất), \(\widehat A = 3\widehat B\)
Theo định lí tổng các góc trong tứ giác ta có:
\(\widehat A + \widehat B + \widehat C + \widehat D = 360^\circ \Rightarrow 2\left( {\widehat A + \widehat B} \right) = 360^\circ \Rightarrow \widehat A + \widehat B = 180^\circ \)
\( \Rightarrow 3\widehat B + \widehat B = 180^\circ \Rightarrow \widehat B = 45^\circ \)
\( \Rightarrow \widehat A = 3\widehat B = 3.45^\circ = 135^\circ \)
Vậy \(\widehat A = \widehat C = 135^\circ ;\widehat B = \widehat D = 45^\circ \).

