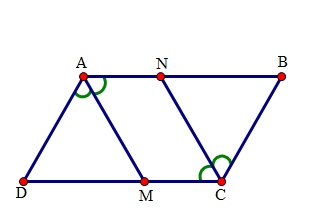
Cho hình bình hành \(ABCD\). Tia phân giác của góc \(A\) cắt \(CD\) tại \(M\). Tia phân giác góc \(C\) cắt \(AB\) tại \(N\) (hình vẽ). Hãy chọn câu trả lời sai.

Vì \(\widehat {NAM} = \dfrac{1}{2}\widehat A,\widehat {MCN} = \dfrac{1}{2}\widehat C\) mà \(\widehat A = \widehat C\) (góc đối hình bình hành) nên \(\widehat {NAM} = \widehat {MCN}\).

Lại có: \(\widehat {BNC} = \widehat {MCN}\) (so le trong, \(AB\parallel CD\)).

Suy ra \(\widehat {NAM} = \widehat {BNC}\).

Mà hai góc \(\widehat {NAM},\widehat {BNC}\) ở vị trí đồng vị nên \(AM\parallel CN\).

Do \(AB\parallel CD(gt),N \in AB,M \in BC \Rightarrow AN\parallel MC\).

Tứ giác \(AMCN\) có \(AN\parallel CM,AM\parallel CN(cmt)\) nên là hình bình hành (dấu hiệu nhận biết).

Vì \(AMCN\) là hình bình hành nên \(AN = CM\) (tính chất) nên A, D đúng.

Vì \(MC//AB \Rightarrow AMCB\) là hình thang nên B đúng.

Vì \(AN//CD \Rightarrow ANCD\) là hình thang.

Chưa đủ điều kiện để \(ANCD\) là hình thang cân nên C sai.