Tính chu vi của tam giác \(AMN\) theo \(a\) .
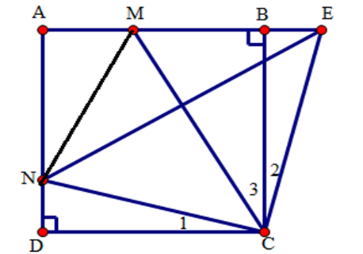
Ta có: \(\Delta CMN = \Delta CME\) (do tính đối xứng qua $CM$ )
Nên $MN = ME$
Suy ra chu vi tam giác \(AMN\) là:
$AM + AN + MN = AM + AN{\rm{ }} + ME = AM + AN + MB + BE$
$ = AM + AN + MB + ND$ (vì \(\Delta CDN = \Delta CBE\) (theo câu trước) nên $BE = ND$)
$ = \left( {AM{\rm{ }} + MB} \right) + \left( {AN + ND} \right) = 2a$
Vậy chu vi tam giác $AMN$ bằng $2a$ .
Chọn kết luận đúng nhất.
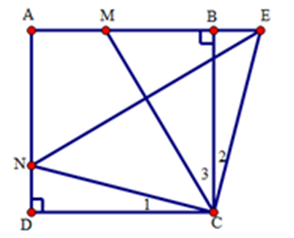
Ta có $CN \bot CE\,\left( {gt} \right)$ mà \(\widehat {MCN} = {45^0}\) nên \(\widehat {MCE} = {45^0}\) hay $\widehat {{C_2}} + \widehat {{C_3}} = {45^0}$. Mà $\widehat {{C_1}} + \widehat {{C_3}} = {45^0}$(vì \(\widehat {MCN} = {45^0}\)) nên $\widehat {{C_1}} = \widehat {{C_2}}$.
Xét tam giác $CDN$ và tam giác $CBE$ có:
$BC = DC$ (do $ABCD$ là hình vuông); \(\widehat D = \widehat B = {90^0}\) ; $\widehat {{C_1}} = \widehat {{C_2}}$(cmt)
Suy ra \(\Delta CDN = \Delta CBE(g.c.g)\) .Suy ra $CN = CE$
Xét tam giác $CEN$ có $CN = CE$ (cmt) nên tam giác $CEN$ là tam giác cân tại $C$.
Suy ra phân giác $CM$ đồng thời là đường trung trực của $NE$ .
Vậy E là điểm đối xứng của $N$ qua $CM$ .
Chọn kết luận đúng nhất.

Ta có $CN \bot CE\,\left( {gt} \right)$ mà \(\widehat {MCN} = {45^0}\) nên \(\widehat {MCE} = {45^0}\) hay $\widehat {{C_2}} + \widehat {{C_3}} = {45^0}$. Mà $\widehat {{C_1}} + \widehat {{C_3}} = {45^0}$(vì \(\widehat {MCN} = {45^0}\)) nên $\widehat {{C_1}} = \widehat {{C_2}}$.
Xét tam giác $CDN$ và tam giác $CBE$ có:
$BC = DC$ (do $ABCD$ là hình vuông); \(\widehat D = \widehat B = {90^0}\) ; $\widehat {{C_1}} = \widehat {{C_2}}$(cmt)
Suy ra \(\Delta CDN = \Delta CBE(g.c.g)\) .Suy ra $CN = CE$
Xét tam giác $CEN$ có $CN = CE$ (cmt) nên tam giác $CEN$ là tam giác cân tại $C$.
Suy ra phân giác $CM$ đồng thời là đường trung trực của $NE$ .
Vậy E là điểm đối xứng của $N$ qua $CM$ .
Chọn kết luận đúng nhất.

Ta có $CN \bot CE\,\left( {gt} \right)$ mà \(\widehat {MCN} = {45^0}\) nên \(\widehat {MCE} = {45^0}\) hay $\widehat {{C_2}} + \widehat {{C_3}} = {45^0}$. Mà $\widehat {{C_1}} + \widehat {{C_3}} = {45^0}$(vì \(\widehat {MCN} = {45^0}\)) nên $\widehat {{C_1}} = \widehat {{C_2}}$.
Xét tam giác $CDN$ và tam giác $CBE$ có:
$BC = DC$ (do $ABCD$ là hình vuông); \(\widehat D = \widehat B = {90^0}\) ; $\widehat {{C_1}} = \widehat {{C_2}}$(cmt)
Suy ra \(\Delta CDN = \Delta CBE(g.c.g)\) .Suy ra $CN = CE$
Xét tam giác $CEN$ có $CN = CE$ (cmt) nên tam giác $CEN$ là tam giác cân tại $C$.
Suy ra phân giác $CM$ đồng thời là đường trung trực của $NE$ .
Vậy E là điểm đối xứng của $N$ qua $CM$ .
Hãy chọn câu đúng.
Đường thẳng đi qua trung điểm hai đáy của hình thang cân là trục đối xứng của hình thang cân đó.
Như vậy hình thang cân có trục đối xứng là đường trung trực của hai đáy.
Cho tam giác \(ABC\) cân tại \(A\), các đường trung tuyến \(AA',BB',CC'\). Trục đối xứng của tam giác \(ABC\) là:
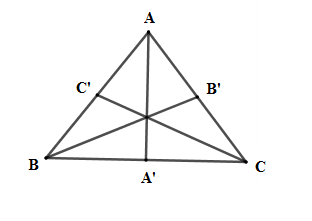
Do tam giác \(ABC\) cân tại \(A\), nên đường trung tuyến \(AA'\) đồng thời là đường trung trực.
Do đó \(AA'\) là trục đối xứng của tam giác \(ABC\).
Cho hình vẽ. Hãy chọn câu sai.
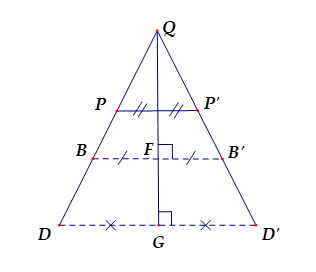
Từ hình vẽ ta có đường thẳng \(QG\) là đường trung trực của đoạn thẳng \(DD',BB',PP'\) nên
Điểm đối xứng với \(P\) qua đường thẳng \(QG\) là \(P'\) nên B đúng.
Điểm đối xứng với \(B\) qua đường thẳng \(QG\) là \(B'\) nên B đúng.
Điểm đối xứng với \(D\) qua đường thẳng \(QG\) là \(D'\) nên C sai.
Vì \(G \in QG\) nên điểm đối xứng với \(G\) qua \(QG\) là \(G\) nên D đúng.
Cho hình vẽ, với \(AD = AE,AG\) là trung trực của \(DE\). Có bao nhiêu cặp đoạn thẳng đối xứng nhau qua trục \(AG\) (các đoạn thẳng thuộc đường thẳng $AD, AE$)? Chọn câu đúng.
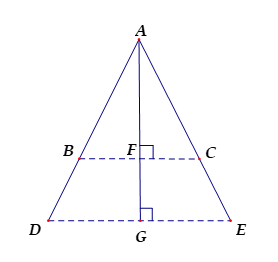
Từ giả thiết ta thấy \(\Delta ADE\) cân tại \(A\) có \(AG\) là đường cao nên \(AG\) cũng là đường trung trực của \(DE.\)
Nên điểm \(D\) và \(E\) đối xứng với nhau qua \(AG\).
Lại có \(BC//DE\) (cùng vuông với \(AG\)) nên suy ra \(\dfrac{{AB}}{{AD}} = \dfrac{{AC}}{{AE}}\) (định lý Ta-lét)
Mà \(AD = AE\left( {gt} \right) \Rightarrow AB = AC\). Do đó \(\Delta ABC\) cân tại \(A\) có \(AF\) là đường cao nên \(AF\) cũng là đường trung trực của \(BC\).
Từ đó điểm \(B,C\) đối xứng nhau qua \(AG\).
Như vậy:
+ Hai đoạn thẳng \(BD,CE\) đối xứng nhau qua \(AG\)
+ Hai đoạn thẳng \(AB,AC\) đối xứng nhau qua \(AG\)
+ Hai đoạn thẳng \(AD,AE\) đối xứng nhau qua \(AG\)
Cho đoạn thẳng \(AB\) có độ dài \(6cm\) và đường thẳng \(d\). Đoạn thẳng \(A'B'\) đối xứng với \(AB\) qua \(d\). Độ dài đoạn thẳng \(A'B'\) là:
Vì đoạn thẳng \(A'B'\) đối xứng với \(AB\) qua \(d\) nên \(A'B' = AB = 6\,cm\).
Cho tam giác \(ABC\) và tam giác \(A'B'C'\) đối xứng nhau qua đường thẳng \(d\) biết \(AB = 8cm,BC = 11cm\) và chu vi của tam giác \(ABC\) bằng \(30\,cm\). Khi đó độ dài cạnh \(C'A'\) của tam giác \(A'B'C'\) là:
+ Xét tam giác \(ABC\) có chu vi \({P_{ABC}} = AB + AC + BC \Rightarrow AC = {P_{ABC}} - AB - BC = 30 - 8 - 11\) \( = 11\,cm\).
+ Vì tam giác \(ABC\) và tam giác \(A'B'C'\) đối xứng nhau qua đường thẳng \(d\) nên \(AC = A'C' = 11\,\,cm\).
Cho tam giác \(ABC\), trong đó \(AB = 8\,cm,AC = 10\,cm\). Vẽ hình đối xứng với tam giác \(ABC\) qua trục là cạnh \(BC\). Chu vi của tứ giác tạo thành là:
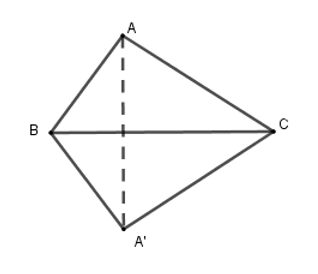
Gọi \(A'\) là điểm đối xứng với \(A\) qua \(BC\). Khi đó tam giác \(A'BC\) đối xứng với tam giác \(ABC\) qua \(BC\).
Tứ giác tạo thành là \(ABCA'\).
Ta có: \(A'B = AB = 8\,cm\) (vì \(A'B\) và \(AB\) đối xứng nhau qua \(BC\)).
\(A'C = AC = 10\,cm\) (vì \(A'C\) và \(AC\) đối xứng nhau qua \(BC\)).
Chu vi tứ giác \(ABCA'\) là \(P = AB + AC + A'B + A'C\)\( = 8 + 10 + 8 + 10 = 36\,cm\).
Tính góc \(BMC\).
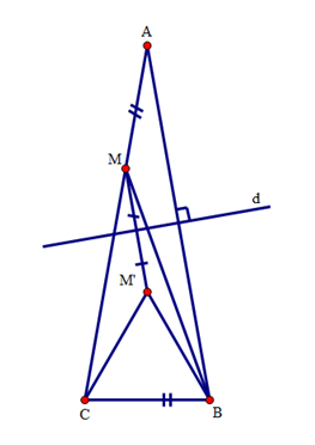
Ta cũng có: \(\widehat {MCB} = {180^0} - \left( {\widehat A + \widehat B} \right) = {180^0} - \left( {{{20}^0} + {{80}^0}} \right) = {80^0}\)
Suy ra \(\widehat {MCM'} = \widehat {MCB} - \widehat {M'CB} = {80^0} - {60^0} = {20^0}\)
Mà \(\widehat {CMM'} = \widehat A = {20^0}\)(góc đồng vị).
Nên \(\widehat {MCM'} = \widehat {CMM'} = {20^ \circ }\)
Suy ra \(M'C = M'M = M'B\).
Ta lại có: \(\widehat {M'MB} = \widehat {M'BM}\) (tam giác \(M'MB\) cân tại đỉnh \(M'\)); \(\widehat {M'MB} = \widehat {MBA}\)(so le trong).
Nên \(\widehat {M'BM} = \widehat {MBA} = \dfrac{1}{2}\widehat {M'BA} = {10^0}\)
Vậy \(\widehat {BMC} = \widehat {CMM'} + \widehat {M'MB} = {20^0} + {10^0} = {30^0}\)
Tam giác \(M'BC\) là tam giác gì? Chọn đáp án đúng nhất.
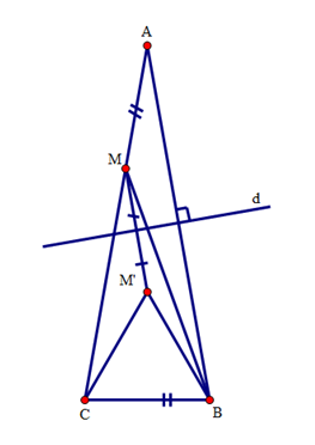
Do tính chất đối xứng qua \(d\), ta có \(AM = BM'\).
Mà \(AM = BC\left( {gt} \right)\) nên \(BM' = BC\).
Ta lại có: \(\widehat {M'BA} = \widehat {MAB} = {20^0}\) (do \(M,{\rm{ }}A\) đối xứng với \(M',{\rm{ }}B\) qua \(d\)).
Suy ra \(\widehat {M'BC} = \widehat B - {20^0} = {80^0} - {20^0} = {60^0}\).
Xét tam giác \(M'BC\) có \(BM' = BC\), \(\widehat {M'BC} = {60^0}\) do đó tam giác \(M'BC\) là tam giác đều.
Tam giác \(M'BC\) là tam giác gì? Chọn đáp án đúng nhất.

Do tính chất đối xứng qua \(d\), ta có \(AM = BM'\).
Mà \(AM = BC\left( {gt} \right)\) nên \(BM' = BC\).
Ta lại có: \(\widehat {M'BA} = \widehat {MAB} = {20^0}\) (do \(M,{\rm{ }}A\) đối xứng với \(M',{\rm{ }}B\) qua \(d\)).
Suy ra \(\widehat {M'BC} = \widehat B - {20^0} = {80^0} - {20^0} = {60^0}\).
Xét tam giác \(M'BC\) có \(BM' = BC\), \(\widehat {M'BC} = {60^0}\) do đó tam giác \(M'BC\) là tam giác đều.
Hãy chọn câu đúng. Trục đối xứng của hình thang cân là:
Đường thẳng đi qua trung điểm hai đáy của hình thang cân là trục đối xứng của hình thang cân đó.
Hãy chọn câu đúng?
+ Hình thang cân có trục đối xứng là đường thẳng đi qua trung điểm hai đáy nên hình thang cân có một trục đối xứng. Do đó A sai.
+ Tam giác cân có một trục đối xứng là đường trung trực hạ từ đỉnh cân nên B sai.
+ Tam giác thường thì không có trục đối xứng nên C sai.
+ Tam giác đều có ba trục đối xứng là ba đường trung trực của tam giác nên D đúng.
Cho tam giác $ABC$ cân tại $B$ , các đường trung tuyến $AA',BB',CC'$ . Trục đối xứng của tam giác $ABC$ là:
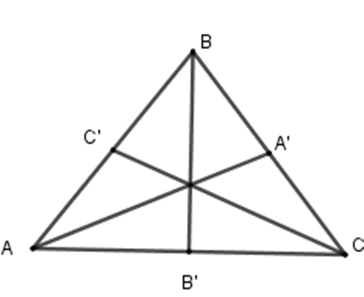
Do tam giác $ABC$ cân tại $B$ , nên đường trung tuyến $BB'$ đồng thời là đường trung trực.
Do đó $BB'$ là trục đối xứng của tam giác $ABC$.
Hãy chọn câu sai:
Vì hai đoạn thẳng (góc, tam giác) đối xứng với nhau qua một đường thẳng thì chúng bằng nhau nên D sai.
Cho hình vẽ. Hãy chọn câu đúng.
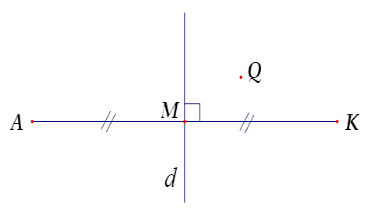
Từ hình vẽ ta có đường thẳng \(d\) là đường trung trực của đoạn thẳng \(AK\) nên Điểm đối xứng với \(A\) qua đường thẳng \(d\) là \(K\).
Hãy chọn câu sai.
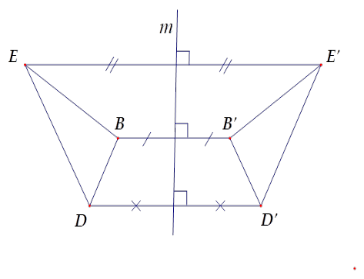
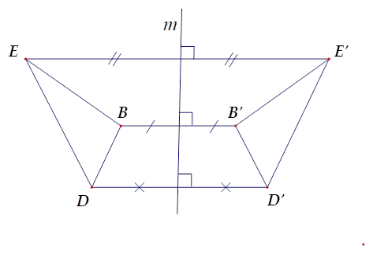
Từ hình vẽ ta có \(A\) và \(A'\) đối xứng nhau qua đường thẳng \(m\); \(B\) và \(B'\) đối xứng nhau qua đường thẳng \(m\); \(C\) và \(C'\) đối xứng nhau qua đường thẳng \(m\).
Suy ra hai đoạn thẳng \(EB\) và \(E'B'\) đối xứng nhau qua \(m\).
Hai đoạn thẳng \(DB\) và \(D'B'\) đối xứng nhau qua \(m\).
Hai tam giác \(DEB\) và \(D'E'B'\) đối xứng nhau qua \(m\).
Hai đoạn thẳng \(DE\) và \(D'E'\) đối xứng nhau qua \(m\) nên D sai.

