Trả lời bởi giáo viên
Đáp án đúng: d
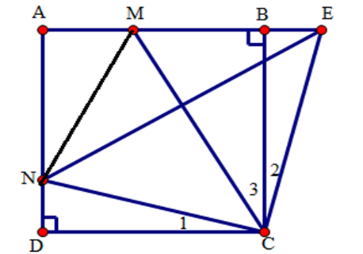
Ta có: \(\Delta CMN = \Delta CME\) (do tính đối xứng qua $CM$ )
Nên $MN = ME$
Suy ra chu vi tam giác \(AMN\) là:
$AM + AN + MN = AM + AN{\rm{ }} + ME = AM + AN + MB + BE$
$ = AM + AN + MB + ND$ (vì \(\Delta CDN = \Delta CBE\) (theo câu trước) nên $BE = ND$)
$ = \left( {AM{\rm{ }} + MB} \right) + \left( {AN + ND} \right) = 2a$
Vậy chu vi tam giác $AMN$ bằng $2a$ .
Hướng dẫn giải:
Bước 1: Ta sử dụng chú ý: “ Nếu hai đoạn thẳng (góc, tam giác) đối xứng với nhau qua một đường thẳng thì chúng bằng nhau.”
Bước 2: Từ đó ta biến đổi các cạnh của tam giác để xuất hiện các cạnh của hình vuông để tính chu vi tam giác \(AMN\) .