Chọn câu đúng. Cho hình vẽ sau. Đường trung bình của tam giác \(ABC\) là:
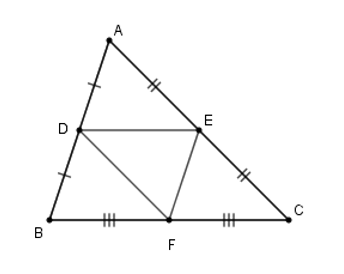
Xét tam giác \(ABC\) có \(D,E,F\) lần lượt là trung điểm các cạnh \(AB,AC,BC\) nên \(DE,DF,EF\) là ba đường trung bình của tam giác \(ABC.\)
Hãy chọn câu đúng?
Cho tam giác \(ABC\) có chu vi là \(80\). Gọi \(E,F,P\) là trung điểm của các cạnh \(AB,BC,CA\). Chu vi của tam giác \(EFP\) là:
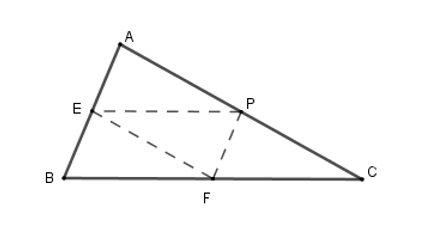
Vì \(E,F,P\) là trung điểm của các cạnh \(AB,BC,CA\) nên \(EF;EP;FP\) là các đường trung bình của tam giác \(ABC\).
Suy ra \(EF = \dfrac{1}{2}AC;\,FP = \dfrac{1}{2}AB;\,EP = \dfrac{1}{2}BC\) \( \Rightarrow EF + FP + EP = \dfrac{1}{2}AC + \dfrac{1}{2}AB + \dfrac{1}{2}BC\)
\( \Leftrightarrow EF + FP + EP = \dfrac{1}{2}\left( {AB + AC + BC} \right)\) hay chu vi tam giác \(EFP = \dfrac{1}{2}\) chu vi tam giác \(ABC\).
Do đó chu vi tam giác \(EFP\) là \(80:2 = 40\).
Một hình thang có đáy lớn là \(8\,cm\), đáy nhỏ ngắn hơn đáy lớn là \(2\,cm\). Độ dài đường trung bình của hình thang là:
+ Vì đáy nhỏ ngắn hơn đáy lớn \(2\,cm\) nên độ dài đáy nhỏ là \(8 - 2 = 6\,cm\).
+ Vì đường trung bình của hình thang bằng nửa tổng hai đáy nên độ dài đường trung bình là \(\dfrac{{8 + 6}}{2} = 7\,cm\).
Hãy chọn câu đúng?
Cho \(\Delta ABC\), \(I,K\) lần lượt là trung điểm của \(AB\) và \(BC\). Biết \(AC = 10\,cm\). Ta có:
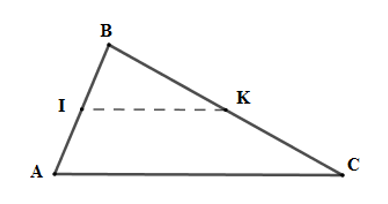
+ Vì \(I,K\) lần lượt là trung điểm của \(AB\) và \(BC\) nên \(IK\) là đường trung bình của tam giác \(ABC \Rightarrow IK = \dfrac{1}{2}AC = \dfrac{1}{2}.10 = 5\,cm\).
Vậy \(IK = 5\,cm\).
Cho \(\Delta ABC\) đều, cạnh \(3cm\); \(M,N\) là trung điểm của \(AB\) và \(AC\). Chu vi của tứ giác \(MNCB\) bằng:
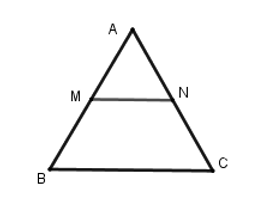
+ \(M,N\) là trung điểm của \(AB\) và \(AC\) nên \(MN\) là đường trung bình của tam giác \(ABC\) \( \Rightarrow MN = \dfrac{1}{2}BC = \dfrac{1}{2}. 3 = 1,5\,cm\).
+ \(MB = \dfrac{{AB}}{2} = \dfrac{3}{2} = 1,5\,\,cm;\,NC = \dfrac{{AC}}{2} = \dfrac{3}{2} = 1,5\,cm\).
+ Chu vi tứ giác \(MNCB\) là \(P = MN + BC + MB + NC\)\( = 1,5 + 1,5 + 1,5 + 3 = 7,5\,cm\).
Tính \(x,y\) trên hình vẽ, trong đó \(AB{\rm{//}}EF{\rm{//}}GH{\rm{//}}CD\). Hãy chọn câu đúng.
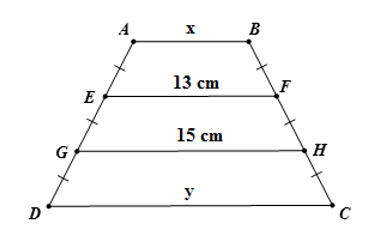
+ Vì \(AB{\rm{//}}EF{\rm{//}}GH{\rm{//}}CD\) nên các tứ giác \(EFCD;\,ABHG\) là hình thang.
+ Từ hình vẽ ta có \(GH\) là đường trung bình của hình thang \(EFCD \Rightarrow HG = \dfrac{{EF + CD}}{2}\).
Hay \(\dfrac{{y + 13}}{2} = 15\, \Leftrightarrow y = 2.15 - 13 = 17\)
Vậy \(y = 17\,\).
+ Lại có \(EF\) là đường trung bình của hình thang \(ABHG \Rightarrow EF = \dfrac{{AB + HG}}{2}\)
\( \Rightarrow 13 = \dfrac{{AB + 15}}{2} \Rightarrow x + 15 = 26 \Rightarrow x = 11\,\) hay \(x = 11\,\).
Vậy \(x = 11\,;\,y = 17\,\) .
Cho tam giác \(ABC\), đường trung tuyến \(AM\). Gọi \(D\) là trung điểm của \(AM,E\) là giao điểm của \(BD\) và \(AC,F\) là trung điểm của \(EC\). Tính \(AE\) biết \(AC = 9cm\).

Xét tam giác \(BEM\) có \(BM = MC,EF = FC\) nên \(MF\) là đường trung bình của tam giác \(BEC\). Do đó \(MF{\rm{//}}BE\).
Xét tam giác \(AMF\) có \(AD = DM,DE//MF\) nên \(DE\) là đường trung bình của tam giác \(AMF\). Do đó \(AE = EF\).
Do đó \(AE = EF = FC\) nên \(AE = \dfrac{1}{3}AC = \dfrac{1}{3}. 9 = 3cm\).
Cho tam giác \(ABC\), các đường trung tuyến \(BD\) và \(CE\) cắt nhau ở \(G\). Gọi \(I,K\) theo thứ tự là trung điểm của \(GB,GC\). Tính \(EI;DK\) biết \(AG = 4\,cm\).
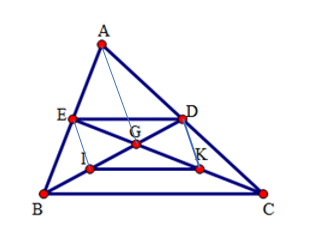
Vì tam giác \(ABG\) có \(AE = EB,IB = IG\) nên \(EI\) là đường trung bình, do đó \(EI = \dfrac{1}{2}AG\).
Tương tự tam giác \(AGC\) có \(AD = DC,GK = KC\) nên \(DK\) là đường trung bình, do đó \(DK = \dfrac{1}{2}AG\).
Suy ra \(EI = DK = \dfrac{1}{2}AG = \dfrac{1}{2}. 4 = 2cm\).
Tính độ dài đường trung bình của hình thang cân, biết rằng hai đường chéo vuông góc với nhau và đường cao của nó bằng \(15cm\).
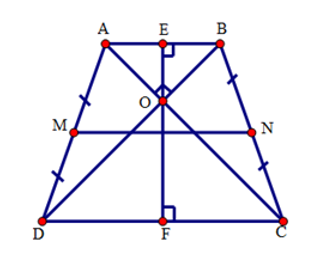
+ Xét hình thang cân \(ABCD\left( {AB//CD} \right)\), hai đường chéo \(AC\) và \(BD\) vuông góc với nhau tại \(O,{\rm{ }}MN\) là đường trung bình của hình thang \(ABCD\). Qua \(O\) kẻ đường thẳng vuông góc với \(AB\) tại \(E\), với \(CD\) tại \(F\).
Xét \(\Delta ADC\) và \(\Delta BCD\) có:
\(AD = BC\) (gt)
DC cạnh chung
\(\widehat {ADC} = \widehat {BCD}\) (gt)
\( \Rightarrow \Delta ADC = \Delta BCD(c.g.c) \Rightarrow \widehat {ACD} = \widehat {BDC}\) ( hai góc tương ứng)\( \Rightarrow \Delta OCD\) cân tại O\( \Rightarrow OC = OD\).
Mà \(AC = BD\) nên \(OA = OB \Rightarrow \Delta OAB\) cân tại \(O\).
Lại có: \(\widehat {AOB} = 90^\circ \) ( do \(AB\) vuông góc với \(CD\)) nên \(\Delta AOB\) vuông cân tại \(O\) nên \(OE = \dfrac{{AB}}{2}\).
Tương tự: tam giác \(DOC\) vuông cân tại \(O\) nên \(FO = \dfrac{{CD}}{2}\).
Do đó \(FE = \dfrac{{AB + CD}}{2}\)
\(MN\) là đường trung bình của hình thang \(ABCD\) nên \(MN = \dfrac{{AB + CD}}{2}\).
\( \Rightarrow MN = FE = 15cm\).
Cho tam giác \(ABC\), điểm \(D\) thuộc cạnh \(AC\) sao cho \(AD = \dfrac{1}{2}DC\). Gọi \(M\) là trung điểm của \(BC,I\) là giao điểm của \(BD\) và \(AM\). Tính \(AM\) biết \(IM = 3\,cm\).
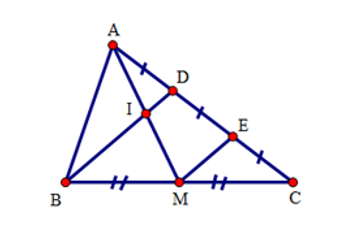
Gọi \(E\) là trung điểm của \(DC\).
Xét tam giác \(BDC\) có: \(BM = MC,DE = EC\) nên \(ME\) là đường trung bình của tam giác\(BDC\) . Suy ra \(BD//ME\) hay \(DI//EM\).
Xét tam giác \(AME\) có \(AD = DE,DI//EM\) nên \(AI\; = IM\).
Suy ra \(AM = 2IM = 2.3 = 6\,cm\).
Độ dài đường trung bình của hình thang là \(20cm\); hai đáy tỉ lệ với \(2\) và \(3\) thì độ dài hai đáy là:
Gọi \(a\) và \(b\) lần lượt là độ dài hai đáy nhỏ, đáy lớn của hình thang.
Theo định lí đường trung bình của hình thang suy ra \(a + b = 2.20 = 40(cm)\).
Mặt khác theo bài ra \(a\) và \(b\) tỉ lệ với \(2\) và \(3\) nên ta có: \(\dfrac{a}{2} = \dfrac{b}{3}\).
Theo định lý của dãy tỉ số bằng nhau ta có:
\(\dfrac{a}{2} = \dfrac{b}{3} = \dfrac{{a + b}}{{2 + 3}} = \dfrac{{40}}{5} = 8\) \( \Rightarrow a = 8.2 = 16(cm)\) và \(b = 8.3 = 24(cm)\).
Vậy độ dài \(2\) đáy của hình thang là \(16cm,{\rm{ }}24cm\).
Hãy chọn câu đúng. Cho hình thang \(ABCD\) có \(AB//CD\). Lấy \(M,N\) lần lượt là trung điểm của \(AD,BC\). Khi đó:
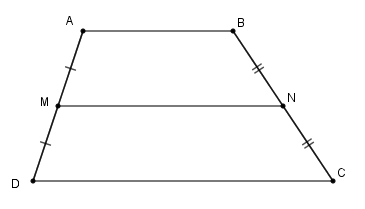
Từ giả thiết ta thấy \(MN\) là đường trung bình của hình thang \(ABCD\).
Suy ra \(MN = \dfrac{{AB + CD}}{2}\).
Chọn câu đúng.
+ Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác nên B đúng.
+ Đường trung bình của hình thang là đoạn thẳng nối trung điểm hai cạnh bên của hình thang nên A, D sai.
+ Trong một tam giác có ba đường trung bình nên C sai.
Hãy chọn câu sai
+ Độ dài đường trung bình hình thang bằng nửa tổng hai đáy nên đáp án B sai.
Hãy chọn câu đúng?
Cho tam giác \(ABC\) có chu vi là \(32\) cm. Gọi \(E,F,P\) là trung điểm của các cạnh \(AB,BC,CA\). Chu vi của tam giác \(EFP\) là
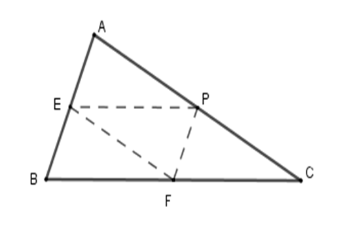
Vì \(E,F,P\) là trung điểm của các cạnh \(AB,BC,CA\) nên \(EF;EP;FP\) là các đường trung bình của tam giác \(ABC\) .
Suy ra \(EF = \dfrac{1}{2}AC;\,FP = \dfrac{1}{2}AB;\,EP = \dfrac{1}{2}BC\) \( \Rightarrow EF + FP + EP = \dfrac{1}{2}AC + \dfrac{1}{2}AB + \dfrac{1}{2}BC\)
\( \Leftrightarrow EF + FP + EP = \dfrac{1}{2}\left( {AB + AC + BC} \right)\) hay chu vi tam giác \(EFP = \dfrac{1}{2}\) chu vi tam giác \(ABC\) .
Do đó chu vi tam giác \(EFP\) là \(32:2 = 16\) cm .
Một hình thang có đáy lớn là \(5\,cm\), đáy nhỏ ngắn hơn đáy lớn là \(0,8\,cm\). Độ dài đường trung bình của hình thang là
+ Vì đáy nhỏ ngắn hơn đáy lớn \(0,8\,cm\) nên độ dài đáy nhỏ là \(5 - 0,8 = 4,2\,cm\) .
+ Vì đường trung bình của hình thang bằng nửa tổng hai đáy nên độ dài đường trung bình là \(\dfrac{{5 + 4,2}}{2} = 4,6\,cm\) .
Hãy chọn câu đúng?
Cho \(\Delta ABC\), \(I,K\) lần lượt là trung điểm của \(AB\) và \(AC\). Biết \(BC = 8\,cm,AC = 7\,cm\). Ta có:
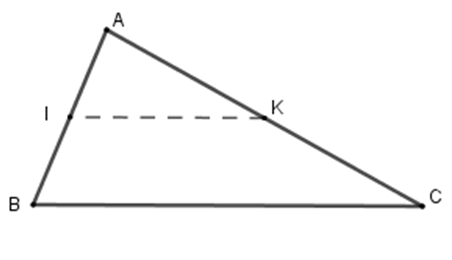
+ Vì \(I,K\) lần lượt là trung điểm của \(AB\) và \(AC\) nên \(IK\) là đường trung bình của tam giác \(ABC \)\(\Rightarrow IK = \dfrac{1}{2}BC = \dfrac{1}{2}.8 = 4\,cm\) .
Vậy \(IK = 4\,cm\) .
Cho \(\Delta ABC\) đều, cạnh \(2cm\); \(M,N\) là trung điểm của \(AB\) và \(AC\). Chu vi của tứ giác \(MNCB\) bằng
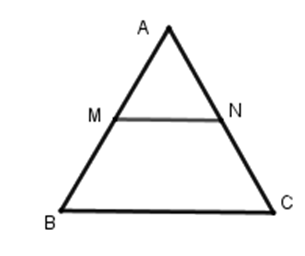
+ \(M,N\) là trung điểm của \(AB\) và \(AC\)nên \(MN\) là đường trung bình của tam giác \(ABC\) \( \Rightarrow MN = \dfrac{1}{2}BC = \dfrac{1}{2}.2 = 1\,cm\) .
+ \(MB = \dfrac{{AB}}{2} = \dfrac{2}{2} = 1\,cm;\,NC = \dfrac{{AC}}{2} = \dfrac{2}{2} = 1\,cm\)
+ Chu vi tứ giác \(MNCB\) là \(P = MN + BC + MB + NC\)\( = 1 + 1 + 1 + 2 = 5\,cm\) .
Tính \(x,y\) trên hình vẽ, trong đó \(AB{\rm{//}}EF{\rm{//}}GH{\rm{//}}CD\). Hãy chọn câu đúng.
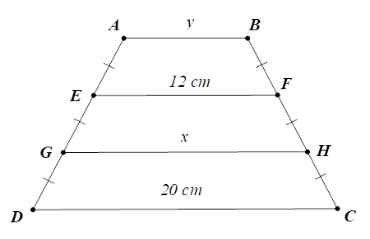
+ Vì \(AB{\rm{//}}EF{\rm{//}}GH{\rm{//}}CD\) nên các tứ giác \(EFCD;\,ABHG\) là hình thang.
+ Từ hình vẽ ta có \(GH\) là đường trung bình của hình thang \(EFCD \Rightarrow HG = \dfrac{{EF + CD}}{2}\) \( = \dfrac{{12 + 20}}{2} = 16\,cm\) .
Hay \(x = 16\,cm\) .
+ Lại có \(EF\) là đường trung bình của hình thang \(ABHG \Rightarrow EF = \dfrac{{AB + HG}}{2}\)
\( \Rightarrow 12 = \dfrac{{AB + 16}}{2} \Rightarrow AB + 16 = 24 \Rightarrow AB = 8\,cm\) hay \(y = 8\,cm\) .
Vậy \(x = 16\,cm;\,y = 8\,cm\) .
Độ dài đường trung bình của hình thang là $16cm$; hai đáy tỉ lệ với $3$ và $5$ thì độ dài hai đáy là :
Gọi $a$ và $b$ lần lượt là độ dài hai đáy nhỏ, đáy lớn của hình thang.
Theo định lí đường trung bình của hình thang suy ra \(a + b = 2.16 = 32(cm)\).
Mặt khác theo bài ra $a$ và $b$ tỉ lệ với $3$ và $5$ nên ta có: \(\dfrac{a}{3} = \dfrac{b}{5}\) .
Theo định lý của dãy tỉ số bằng nhau ta có:
\(\dfrac{a}{3} = \dfrac{b}{5} = \dfrac{{a + b}}{{3 + 5}} = \dfrac{{32}}{8} = 4\) \( \Rightarrow a = 4.3 = 12(cm)\) và \(b = 4.5 = 20(cm)\).
Vậy độ dài $2$ đáy của hình thang là $12cm,{\rm{ }}20cm$ .

