Câu hỏi:
2 năm trước
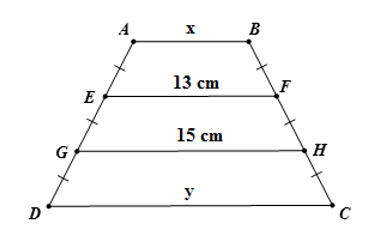
Tính \(x,y\) trên hình vẽ, trong đó \(AB{\rm{//}}EF{\rm{//}}GH{\rm{//}}CD\). Hãy chọn câu đúng.
Trả lời bởi giáo viên
Đáp án đúng: b
+ Vì \(AB{\rm{//}}EF{\rm{//}}GH{\rm{//}}CD\) nên các tứ giác \(EFCD;\,ABHG\) là hình thang.
+ Từ hình vẽ ta có \(GH\) là đường trung bình của hình thang \(EFCD \Rightarrow HG = \dfrac{{EF + CD}}{2}\).
Hay \(\dfrac{{y + 13}}{2} = 15\, \Leftrightarrow y = 2.15 - 13 = 17\)
Vậy \(y = 17\,\).
+ Lại có \(EF\) là đường trung bình của hình thang \(ABHG \Rightarrow EF = \dfrac{{AB + HG}}{2}\)
\( \Rightarrow 13 = \dfrac{{AB + 15}}{2} \Rightarrow x + 15 = 26 \Rightarrow x = 11\,\) hay \(x = 11\,\).
Vậy \(x = 11\,;\,y = 17\,\) .
Hướng dẫn giải:
Ta sử dụng định lý đường trung bình của hình thang để tính độ dài \(x;\,y\).
Đường trung bình hình thang thì song song với hai đáy và bằng nửa tổng hai đáy.
