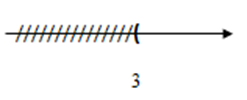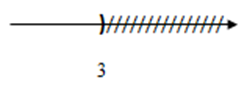Cho các bất phương trình sau, đâu là bất phương trình bậc nhất một ẩn
Dựa vào định nghĩa bất phương trình bậc nhất một ẩn ta có:
Đáp án A là bất phương trình bậc nhất một ẩn.
Đáp án B không phải bất phương trình bậc nhất một ẩn vì $a = 0.$
Đáp án C không phải bất phương trình bậc vì có \({x^2}.\)
Đáp án D không phải bất phương trình vì đây là phương trình bậc nhất một ẩn.
Giá trị $x = 2$ là nghiệm của bất phương trình nào sau đây ?
(Trong bài này chúng ta làm theo cách thứ 2) thay \(x = 2\) vào từng bất phương trình:
Đáp án A: \(7 - 2 < 2.2 \Leftrightarrow 5 < 4\) vô lý. Loại đáp án A.
Đáp án B: \(2.2 + 3 > 9 \Leftrightarrow 7 > 9\) vô lý. Loại đáp án B.
Đáp án C: \( - 4.2 \ge 2 + 5 \Leftrightarrow - 8 \ge 7\) vô lý. Loại đáp án C.
Đáp án D: \(5 - 2 > 6.2 - 12 \Leftrightarrow 3 > 0\) luôn đúng. Chọn đáp án D.
Nghiệm của bất phương trình $7(3x + 5) > 0$ là:
Vì \(7 > 0\) nên \(7\left( {3x + 5} \right) \ge 3 \Leftrightarrow 3x + 5 > 0 \Leftrightarrow 3x > - 5 \Leftrightarrow x > - \dfrac{5}{3}.\)
Cho $a > b$. Bất đẳng thức nào tương đương với bất đẳng thức đã cho?
+) Đáp án A: \(a > b \Leftrightarrow a - 3 > b - 3\)
Vậy ý A đúng chọn luôn ý A.
+) Đáp án B: \( - 3a + 4 > - 3b + 4 \Leftrightarrow - 3a > - 3b \Leftrightarrow a < b\) trái với giả thiết nên B sai.
+) Đáp án C: \(2a + 3 < 2b + 3 \Leftrightarrow 2a < 2b \Leftrightarrow a < b\) trái với giả thiết nên C sai.
+) Đáp án D: \( - 5b - 1 < - 5a - 1 \Leftrightarrow - 5b < - 5a \Leftrightarrow b > a\) trái với giả thiết nên D sai.
Phương trình \(\left| {2x - 5} \right| = 1\) có nghiệm là:
Giải phương trình: \(\left| {2x - 5} \right| = 1\)
$TH1:\;2x - 5 \ge 0 \Leftrightarrow x \ge \dfrac{5}{2} \Rightarrow \left| {2x - 5} \right| = 2x - 5 = 1 \Leftrightarrow 2x = 6 \Leftrightarrow x = 3\;\;\left( {tm} \right)$
$TH2:\;2x - 5 < 0 \Leftrightarrow x < \dfrac{5}{2} \Rightarrow \left| {2x - 5} \right| = - 2x + 5 = 1 \Leftrightarrow 2x = 4 \Leftrightarrow x = 2\;\;\left( {tm} \right)$
Vậy phương trình có hai nghiệm \(x = 3\) và \(\;x = 2\).
Phương trình \(\dfrac{1}{3} - \left| {\dfrac{5}{4} - 2x} \right| = \dfrac{1}{4}\) có nghiệm là
\(\begin{array}{l}\;\;\;\;\;\dfrac{1}{3} - \left| {\dfrac{5}{4} - 2x} \right| = \dfrac{1}{4}\\ \Leftrightarrow \left| {\dfrac{5}{4} - 2x} \right| = \dfrac{1}{3} - \dfrac{1}{4}\\ \Leftrightarrow \left| {\dfrac{5}{4} - 2x} \right| = \dfrac{1}{{12}}\,\left( * \right)\end{array}\)
\(\begin{array}{l}TH1:\;\dfrac{5}{4} - 2x \ge 0 \Leftrightarrow x \le \dfrac{5}{8} \Rightarrow \left| {\dfrac{5}{4} - 2x} \right| = \dfrac{5}{4} - 2x\\ \Rightarrow pt\,\,\left( * \right) \Leftrightarrow \dfrac{5}{4} - 2x = \dfrac{1}{{12}}\\ \Leftrightarrow 2x = \dfrac{7}{6}\\ \Leftrightarrow x = \dfrac{7}{{12}}\;\;\left( {tm} \right)\end{array}\)
\(\begin{array}{l}TH2:\;\;\dfrac{5}{4} - 2x < 0 \Leftrightarrow x > \dfrac{5}{8} \Rightarrow \left| {\dfrac{5}{4} - 2x} \right| = - \dfrac{5}{4} + 2x\;\\ \Rightarrow pt\,\left( * \right) \Leftrightarrow - \dfrac{5}{4} + 2x = \dfrac{1}{{12}}\\ \Leftrightarrow 2x = \dfrac{4}{3}\\ \Leftrightarrow x = \dfrac{2}{3}\;\;\left( {tm} \right).\;\end{array}\)
Vậy phương trình có hai nghiệm \(x = \dfrac{7}{{12}}\) và \(x = \dfrac{2}{3}\).
Hình vẽ dưới đây là biểu diễn tập nghiệm của bất phương trình nào?
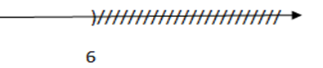
Theo đề bài thì trục số biểu diễn tập nghiệm \(x < 6.\)
Ta có
+) Đáp án A: $x - 1 \ge 5 \Leftrightarrow x \ge 6$ loại vì tập nghiệm là \(x < 6.\)
+) Đáp án B: \(x + 1 \le 7 \Leftrightarrow x \le 6\) loại vì tập nghiệm là \(x < 6.\)
+) Đáp án C: \(x + 3 < 9 \Leftrightarrow x < 6\) thỏa mãn vì tập nghiệm là \(x < 6.\)
+) Đáp án D: \(x + 1 > 7 \Leftrightarrow x > 6\) loại vì tập nghiệm là \(x < 6.\)
Với giá trị nào của $m$ thì bất phương trình $m(2x + 1) < 8$ là bất phương trình bậc nhất một ẩn?
Ta có: $m(2x + 1) < 8 \Leftrightarrow 2mx + m < 8 \Leftrightarrow 2mx + m - 8 < 0$.
Vậy để bất phương trình \(m\left( {2x + 1} \right) < 8\) là bất phương trình bậc nhất 1 ẩn thì \(2mx + m - 8 < 0\) là bất phương trình bậc nhất một ẩn.
Theo định nghĩa bất phương trình bậc nhất một ẩn thì \(a \ne 0\) hay \(2m \ne 0\) $\Leftrightarrow m \ne 0$
Tập nghiệm của bất phương trình $3x + 7 > x + 9$ là
\(3x + 7 > x + 9 \Leftrightarrow 3x - x > 9 - 7 \Leftrightarrow 2x > 2 \Leftrightarrow x >1\)
Vậy tập nghiệm của bất phương trình là $S = \left\{ {x|x > 1} \right\}$
Phương trình \(\left| {5x - 4} \right| = \left| {x + 2} \right|\) có nghiệm là
$\begin{array}{l}\;\;\;\;\left| {5x - 4} \right| = \left| {x + 2} \right|\\ \Leftrightarrow \left[ \begin{array}{l}5x - 4 = x + 2\\5x - 4 = - x - 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}4x = 6\\6x = 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{6}{4} = 1,5\\x = \dfrac{2}{6} = \dfrac{1}{3}\end{array} \right..\end{array}$
Tổng các nghiệm của phương trình \(7,5 - 3\left| {5 - 2x} \right| = - 4,5\) là
\(\begin{array}{l}\;7,5 - 3\left| {5 - 2x} \right| = - 4,5\\ \Leftrightarrow 3\left| {5 - 2x} \right| = 7,5 + 4,5\\ \Leftrightarrow 3\left| {5 - 2x} \right| = 12\\ \Leftrightarrow \left| {5 - 2x} \right| = 4\\ \Leftrightarrow \left[ \begin{array}{l}5 - 2x = 4\\5 - 2x = - 4\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}2x = 1\\2x = 9\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{1}{2}\\x = \dfrac{9}{2}\end{array} \right..\end{array}\)
Vậy nghiệm của phương trình là \(x = \dfrac{1}{2};x = \dfrac{9}{2}\)
Nên tổng các nghiệm của phương trình là \(\dfrac{1}{2} + \dfrac{9}{2} = 5.\)
Số nghiệm của phương trình \(\left| {2x - 3} \right| - \left| {3x + 2} \right| = 0\) là
\(\begin{array}{l}\;\left| {2x - 3} \right| - \left| {3x + 2} \right| = 0\\ \Leftrightarrow \left| {2x - 3} \right| = \left| {3x + 2} \right|\\ \Leftrightarrow \left[ \begin{array}{l}2x - 3 = 3x + 2\\2x - 3 = - (3x + 2)\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - 5\\5x = 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - 5\\x = \dfrac{1}{5}\end{array} \right..\end{array}\)
Vậy phương trình có hai nghiệm là \(x = - 5;x = \dfrac{1}{5}\)
Hình vẽ nào dưới đây biểu diễn tập nghiệm của bất phương trình $2x - 8 \le 13 - 5x.$
$2x - 8 \le 13 - 5x \Leftrightarrow 2x + 5x \le 13 + 8 \Leftrightarrow 7x \le 21 \Leftrightarrow x \le 21:7 \Leftrightarrow x \le 3$
Vậy tập nghiệm của phương trình \(S = \left\{ {x/x \le 3} \right\}\)
Biểu diễn tập nghiệm trên trục số
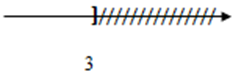
Nghiệm của phương trình \(\left| {x - 1} \right| = 3x - 2\) là:
\(\left| {x - 1} \right| = 3x - 2\)
* Xét \(x - 1 \ge 0 \Leftrightarrow x \ge 1 \Rightarrow Pt \Leftrightarrow x - 1 = 3x - 2\)\( \Leftrightarrow 2x = 1 \Leftrightarrow x = \dfrac{1}{2}\) (KTMĐK)
* Xét \(x - 1 < 0 \Leftrightarrow x < 1 \Rightarrow PT \Leftrightarrow - x + 1 = 3x - 2 \)\(\Leftrightarrow 4x = 3 \Leftrightarrow x = \dfrac{3}{4}\) (TMĐK)
Vậy phương trình có một nghiệm \(x = \dfrac{3}{4}\) .
Số nguyên lớn nhất thỏa mãn bất phương trình ${(x - 2)^2} - {x^2} - 8x + 3 \ge 0$ là
\(\begin{array}{l}{(x - 2)^2} - {x^2} - 8x + 3 \ge 0\\ \Leftrightarrow {x^2} - 4x + 4 - {x^2} - 8x + 3 \ge 0\\ \Leftrightarrow - 12x + 7 \ge 0\\ \Leftrightarrow x \le \dfrac{{ 7}}{{12}}\end{array}\)
Vậy nghiệm của bất phương trình là \(x \le \dfrac{7}{{12}}.\)
Nên số nguyên lớn nhất thỏa mãn bất phương trình là \(x = 0.\)
Số nguyên nhỏ nhất thỏa mãn bất phương trình $x(5x + 1) + 4(x + 3) > 5{x^2}$ là
\(\begin{array}{l}\;x(5x + 1) + 4(x + 3) > 5{x^2}\\ \Leftrightarrow 5{x^2} + x + 4x + 12 > 5{x^2}\\ \Leftrightarrow 5x > - 12\\ \Leftrightarrow x > \dfrac{{ - 12}}{5}\end{array}\)
Vậy nghiệm của bất phương trình là \(x > - \dfrac{{12}}{5}.\)
Số nguyên lớn nhất thỏa mãn bất phương trình là \(x = - 2.\)
Bất phương trình $\dfrac{{3x + 5}}{2} - 1 \le \dfrac{{x + 2}}{3} + x$ có nghiệm là:
Ta có:
$\begin{array}{l}\;\;\;\dfrac{{3x + 5}}{2} - 1 \le \dfrac{{x + 2}}{3} + x\\ \Leftrightarrow \dfrac{{3(3x + 5)}}{6} - \dfrac{6}{6} \le \dfrac{{2(x + 2)}}{6} + \dfrac{{6x}}{6}\\ \Leftrightarrow 3(3x + 5) - 6 \le 2(x + 2) + 6x\\ \Leftrightarrow 9x + 15 - 6 \le 2x + 4 + 6x\\ \Leftrightarrow 9x - 2x - 6x \le 4 - 15 + 6\\ \Leftrightarrow x \le - 5.\end{array}$
Vậy nghiệm của bất phương trình là \(x \le - 5.\)
Bất phương trình $2(x - 1) - x > 3(x - 1) - 2x - 5$ có nghiệm là:
Ta có:
$\begin{array}{l}\;\;\;\;\;2(x - 1) - x > 3(x - 1) - 2x - 5\\ \Leftrightarrow 2x - 2 - x > 3x - 3 - 2x - 5\\ \Leftrightarrow x - 2 > x - 8\\ \Leftrightarrow - 2 > - 8\end{array}$
Luôn đúng
Vậy bất phương trình trên có vô số nghiệm.
Tập nghiệm của bất phương trình \(\dfrac{{x - 3}}{{x + 4}} < 0\) là
Xét \(\dfrac{{x - 3}}{{x + 4}} < 0.\)
Trường hợp 1:
\(\left\{ \begin{array}{l}x - 3 < 0\\x + 4 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x < 3\\x > - 4\end{array} \right. \Leftrightarrow - 4 < x < 3.\)
Trường hợp 2:
\(\left\{ \begin{array}{l}x - 3 > 0\\x + 4 < 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x > 3\\x < - 4\end{array} \right. \Rightarrow \) Bất phương trình vô nghiệm.
Vậy \( - 4 < x < 3.\)
Tìm giá trị của x để biểu thức $A = \dfrac{{5 - 2x}}{{{x^2} + 4}}$ có giá trị dương
Xét $A = \dfrac{{5 - 2x}}{{{x^2} + 4}}$
A có giá trị dương \( \Leftrightarrow A > 0.\)
Ta có: \({x^2} \ge 0\;\forall x \Rightarrow {x^2} + 4 > 0\;\forall x \Rightarrow A > 0 \Leftrightarrow 5 - 2x > 0 \Leftrightarrow x < \dfrac{5}{2}.\)
Vậy với $x < \dfrac{5}{2}$ thì A có giá trị dương.