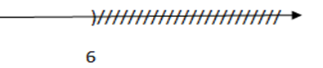Câu hỏi:
3 năm trước
Bất phương trình $\dfrac{{3x + 5}}{2} - 1 \le \dfrac{{x + 2}}{3} + x$ có nghiệm là:
Trả lời bởi giáo viên
Đáp án đúng: d
Ta có:
$\begin{array}{l}\;\;\;\dfrac{{3x + 5}}{2} - 1 \le \dfrac{{x + 2}}{3} + x\\ \Leftrightarrow \dfrac{{3(3x + 5)}}{6} - \dfrac{6}{6} \le \dfrac{{2(x + 2)}}{6} + \dfrac{{6x}}{6}\\ \Leftrightarrow 3(3x + 5) - 6 \le 2(x + 2) + 6x\\ \Leftrightarrow 9x + 15 - 6 \le 2x + 4 + 6x\\ \Leftrightarrow 9x - 2x - 6x \le 4 - 15 + 6\\ \Leftrightarrow x \le - 5.\end{array}$
Vậy nghiệm của bất phương trình là \(x \le - 5.\)
Hướng dẫn giải:
- Áp dụng quy tắc chuyển vế
- Quy đồng bỏ mẫu
- Tìm $x$