Cho tam giác \(ABC\). Gọi \(M,N\) lần lượt là trung điểm của các cạnh \(AB,AC\). Vẽ \(BP \bot MN;\,CQ \bot MN\,\left( {P,\,Q \in MN} \right)\). Biết \({S_{ABC}} = 50\,c{m^2}\), tính \({S_{BPQC}}\).
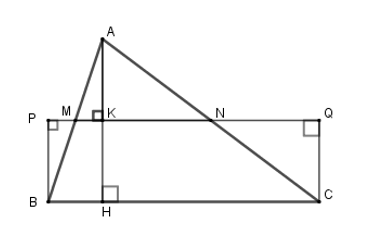
Kẻ \(AH \bot BC\) tại \(H\) và \(AH\) cắt \(MN\) tại \(K\).
+ Xét tam giác \(ABC\) có: \(MN\) là đường trung bình nên \(MN{\rm{//}}BC\) suy ra \(AH \bot MN\) tại \(K\).
Xét tứ giác \(CBPQ\) có: \(PQ{\rm{//}}BC\) (do \(MN{\rm{//}}BC\)) và \(PB{\rm{//}}CQ\) (do cùng vuông góc với \(PQ\) ) nên \(CBPQ\) là hình bình hành. Lại có: \(\widehat {PBC} = 90^\circ \) nên tứ giác \(CBPQ\) là hình chữ nhật.
Suy ra: \({S_{CBPQ}} = BP.BC\)
+ Xét \(\Delta BPM\) và \(\Delta AKM\) có:
Suy ra: \(\Delta BPM = \Delta AKM\,\left( {ch - gn} \right) \Rightarrow BP = AK\) (hai cạnh tương ứng) (1)
Xét \(\Delta ABK\) có: \(MK{\rm{//}}BH\) (do\(MN{\rm{//}}BC\) ) và \(M\) là trung điểm của \(AB\) nên \(K\) là trung điểm của \(AH\) (định lý về đường trung bình của tam giác). Nên \(AK = \dfrac{1}{2}AH\) (2)
Từ (1) và (2) ta có: \(PB = \dfrac{1}{2}AH\).
+ \({S_{ABC}} = \dfrac{1}{2}AH.BC\) mà \(PB = \dfrac{1}{2}AH\)(cmt) nên \({S_{ABC}} = PB.BC\).
Lại có: \({S_{CBPQ}} = BP.BC\) (cmt) nên ta có \({S_{CBPQ}} = {S_{ABC}} = 50\,c{m^2}.\)
Cho tam giác \(ABC\) vuông tại \(A\). Về phía ngoài tam giác, vẽ các hình vuông\(ABDE,ACFG,BCHI\). Biết \({S_{BCHI}} = 100\,c{m^2},\) tính \({S_{ACFG}} + {S_{ABDE}}.\)
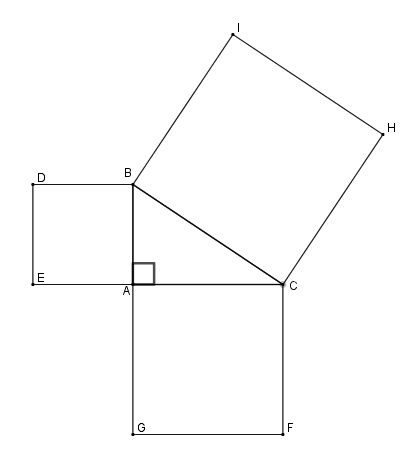
Ta có: \({S_{BCHI}} = B{C^2};\,{S_{ACFG}} = A{C^2};\,{S_{ABDE}} = A{B^2}\).
Theo định lý Pytago cho tam giác \(ABC\) vuông tại \(A\) ta có: \(B{C^2} = A{B^2} + A{C^2}\) \( \Rightarrow {S_{BCHI}} = {S_{ACFG}} + {S_{ABDE}}\).
Vậy \({S_{ACFG}} + {S_{ABDE}} = {S_{BCHI}} = 100\,c{m^2}\).
Tính tỉ số diện tích của tứ giác $ABCD$ và hình thoi $MNPQ$ .
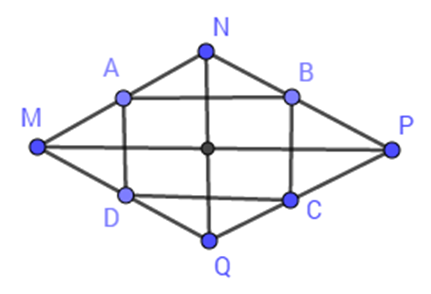
Xét tam giác $MNP$ có: \(MA = AN;\,NB = BP(gt) \Rightarrow \) $AB$ là đường trung bình của tam giác $MNP$ \( \Rightarrow AB = \dfrac{1}{2}MP;\,AB{\rm{//}}MP\,(1)\) (tính chất đường trung bình của tam giác).
Xét tam giác $MQP$ có: \(MD = DQ;\,PC = CQ(gt) \Rightarrow \) $CD$ là đường trung bình của tam giác $MQP$ \( \Rightarrow CD = \dfrac{1}{2}MP;\,CD{\rm{//}}MP\,(2)\) (tính chất đường trung bình của tam giác).
Xét tam giác $MNQ$ có: \(MA = AN;\,MD = DQ(gt) \Rightarrow \) $AD$ là đường trung bình của tam giác $MNQ$ \( \Rightarrow AD = \dfrac{1}{2}NQ;\,AD{\rm{//}}NQ\) (tính chất đường trung bình của tam giác).
Từ (1) và (2) suy ra \(AB = CD;AB{\rm{//}}CD \Rightarrow \) $ABCD$ là hình bình hành (dhnb).
Ta có: \(AB{\rm{//}}MP(cmt);\,NQ \bot MP(gt) \Rightarrow AB \bot NQ\) . Mặt khác \(AD{\rm{//}}NQ\,\,(cmt)\) , suy ra \(AD \bot AB \Rightarrow \widehat {DAB} = 90^\circ \)
Hình bình hành $ABCD$ có \(\widehat {DAB} = 90^\circ \) nên là hình chữ nhật (dhnb).
Diện tích hình thoi $MNPQ$ là: \({S_{MNPQ}} = \dfrac{1}{2}MP.NQ\,(3)\)
Diện tích hình chữ nhật $ABCD$ là: \({S_{ABCD}} = AB.AD = \dfrac{1}{2}MP.\dfrac{1}{2}NQ = \dfrac{1}{4}MP.NQ\,\,(4)\)
Từ (3) và (4) suy ra \(\dfrac{{{S_{ABCD}}}}{{{S_{MNPQ}}}} = \dfrac{1}{2}\) .
Chọn câu sai.
+ Diện tích hình thang bằng nửa tích của tổng hai đáy với chiều cao: \(S = \dfrac{{\left( {a + b} \right)h}}{2}\)
+ Diện tích hình bình hành bằng tích một cạnh với chiều cao ứng với cạnh đó: \(S = a.h\)
+ Diện tích hình thoi bằng nửa tích hai đường chéo: \(S = \dfrac{1}{2}{d_1}.{d_2}\)
Cho diện tích hình thoi $MNPQ$ bằng \(30\,c{m^2}\) , tính diện tích tứ giác $ABCD$ .
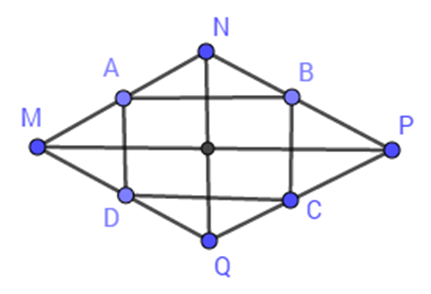
Ta có:\(\dfrac{{{S_{ABCD}}}}{{{S_{MNPQ}}}} = \dfrac{1}{2} \Rightarrow {S_{ABCD}} = \dfrac{1}{2}{S_{MNPQ}} = \dfrac{1}{2}.30 = 15\left( {c{m^2}} \right)\) .
Tính tỉ số diện tích của tứ giác $ABCD$ và hình thoi $MNPQ$ .

Xét tam giác $MNP$ có: \(MA = AN;\,NB = BP(gt) \Rightarrow \) $AB$ là đường trung bình của tam giác $MNP$ \( \Rightarrow AB = \dfrac{1}{2}MP;\,AB{\rm{//}}MP\,(1)\) (tính chất đường trung bình của tam giác).
Xét tam giác $MQP$ có: \(MD = DQ;\,PC = CQ(gt) \Rightarrow \) $CD$ là đường trung bình của tam giác $MQP$ \( \Rightarrow CD = \dfrac{1}{2}MP;\,CD{\rm{//}}MP\,(2)\) (tính chất đường trung bình của tam giác).
Xét tam giác $MNQ$ có: \(MA = AN;\,MD = DQ(gt) \Rightarrow \) $AD$ là đường trung bình của tam giác $MNQ$ \( \Rightarrow AD = \dfrac{1}{2}NQ;\,AD{\rm{//}}NQ\) (tính chất đường trung bình của tam giác).
Từ (1) và (2) suy ra \(AB = CD;AB{\rm{//}}CD \Rightarrow \) $ABCD$ là hình bình hành (dhnb).
Ta có: \(AB{\rm{//}}MP(cmt);\,NQ \bot MP(gt) \Rightarrow AB \bot NQ\) . Mặt khác \(AD{\rm{//}}NQ\,\,(cmt)\) , suy ra \(AD \bot AB \Rightarrow \widehat {DAB} = 90^\circ \)
Hình bình hành $ABCD$ có \(\widehat {DAB} = 90^\circ \) nên là hình chữ nhật (dhnb).
Diện tích hình thoi $MNPQ$ là: \({S_{MNPQ}} = \dfrac{1}{2}MP.NQ\,(3)\)
Diện tích hình chữ nhật $ABCD$ là: \({S_{ABCD}} = AB.AD = \dfrac{1}{2}MP.\dfrac{1}{2}NQ = \dfrac{1}{4}MP.NQ\,\,(4)\)
Từ (3) và (4) suy ra \(\dfrac{{{S_{ABCD}}}}{{{S_{MNPQ}}}} = \dfrac{1}{2}\) .
Tính tỉ số diện tích của tứ giác $ABCD$ và hình thoi $MNPQ$ .

Xét tam giác $MNP$ có: \(MA = AN;\,NB = BP(gt) \Rightarrow \) $AB$ là đường trung bình của tam giác $MNP$ \( \Rightarrow AB = \dfrac{1}{2}MP;\,AB{\rm{//}}MP\,(1)\) (tính chất đường trung bình của tam giác).
Xét tam giác $MQP$ có: \(MD = DQ;\,PC = CQ(gt) \Rightarrow \) $CD$ là đường trung bình của tam giác $MQP$ \( \Rightarrow CD = \dfrac{1}{2}MP;\,CD{\rm{//}}MP\,(2)\) (tính chất đường trung bình của tam giác).
Xét tam giác $MNQ$ có: \(MA = AN;\,MD = DQ(gt) \Rightarrow \) $AD$ là đường trung bình của tam giác $MNQ$ \( \Rightarrow AD = \dfrac{1}{2}NQ;\,AD{\rm{//}}NQ\) (tính chất đường trung bình của tam giác).
Từ (1) và (2) suy ra \(AB = CD;AB{\rm{//}}CD \Rightarrow \) $ABCD$ là hình bình hành (dhnb).
Ta có: \(AB{\rm{//}}MP(cmt);\,NQ \bot MP(gt) \Rightarrow AB \bot NQ\) . Mặt khác \(AD{\rm{//}}NQ\,\,(cmt)\) , suy ra \(AD \bot AB \Rightarrow \widehat {DAB} = 90^\circ \)
Hình bình hành $ABCD$ có \(\widehat {DAB} = 90^\circ \) nên là hình chữ nhật (dhnb).
Diện tích hình thoi $MNPQ$ là: \({S_{MNPQ}} = \dfrac{1}{2}MP.NQ\,(3)\)
Diện tích hình chữ nhật $ABCD$ là: \({S_{ABCD}} = AB.AD = \dfrac{1}{2}MP.\dfrac{1}{2}NQ = \dfrac{1}{4}MP.NQ\,\,(4)\)
Từ (3) và (4) suy ra \(\dfrac{{{S_{ABCD}}}}{{{S_{MNPQ}}}} = \dfrac{1}{2}\) .
Điền cụm từ thích hợp vào chỗ trống: “Diện tích hình bình hành bằng tích của …”
Diện tích hình bình hành bằng tích một cạnh với chiều cao ứng với cạnh đó: \(S = a. h\).
Cho hình thoi \(ABCD\), khi đó:
Hình thoi \(ABCD\) có hai đường chéo \(AC,BD\) nên diện tích \({S_{ABCD}} = \dfrac{1}{2}AC.BD\).
Cho hình bình hành \(ABCD\left( {AB{\rm{//}}CD} \right)\), đường cao \(AH = 5\,cm;CD = 9,6\,cm\). Diện tích hình bình hành \(ABCD\) là:
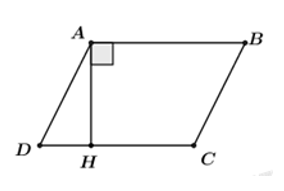
\({S_{ABCD}} = AH.CD = 5 . 9,6 = 48\left( {c{m^2}} \right)\).
Cho hình thang \(ABCD\left( {AB{\rm{//}}CD} \right),\) đường cao \(AH\), \(AB = 5\,cm,CD = 10\,cm,\) diện tích hình thang là \(60\,c{m^2}\) thì \(AH\) bằng:
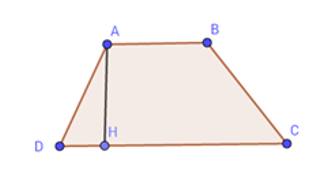
Ta có: \({S_{ABCD}} = \dfrac{{\left( {AB + CD} \right). AH}}{2} \Rightarrow AH = \dfrac{{2{S_{ABCD}}}}{{AB + CD}} = \dfrac{{2.60}}{{10 + 5}} = 8\,(cm)\).
Hai đường chéo hình thoi có độ dài là \(10\,cm\) và \(24\,cm\). Độ dài cạnh hình thoi là:

Giả sử hình thoi \(ABCD\) có đường chéo \(AC\) vuông góc với \(BD\) tại \(O\), \(BD = 10\,cm;\,AC = 24\,cm\).
Suy ra \(BO = \dfrac{1}{2}BD = \dfrac{1}{2}. 12 = 6\,(cm);\,\)\(AO = \dfrac{1}{2}AC = \dfrac{1}{2}. 24 = 12(cm)\).
Áp dụng định lí Py-ta-go trong tam giác vuông \(AOB\) vuông tại \(O\) ta có:
\(AB = \sqrt {A{O^2} + B{O^2}} = \sqrt {{5^2} + {{12}^2}} = 13\,(cm)\).
Cho hình thoi có cạnh là \(10\,cm\), một trong hai đường chéo có độ dài là \(16\,cm\). Diện tích của hình thoi là:
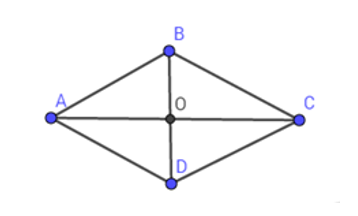
Giả sử hình thoi \(ABCD\), đường chéo \(AC\) vuông góc với \(BD\) tại \(O\), \(AB = 10\,cm;\,\,\,AC = 16\,cm.\)
\(AO = \dfrac{1}{2}AC = \dfrac{1}{2}. 16 = 8\,(cm)\).
Áp dụng định lí Py-ta-go trong tam giác vuông \(AOB\) vuông tại \(O\) ta có:
\(OB = \sqrt {A{B^2} - O{A^2}} = \sqrt {{{10}^2} - {8^2}} = 6\).
\({S_{ABCD}} = \dfrac{1}{2}BD. AC = \dfrac{1}{2}. 2OB. AC\) \( = OB. AC = 6. 16 = 96\left( {c{m^2}} \right)\).
Cho hình thoi \(ABCD\) có hai đường chéo \(AC\) và \(BD\) cắt nhau tại \(O\). Biết \(AB = 20\,cm,OA = 16\,cm\). Diện tích hình thoi \(ABCD\) là:
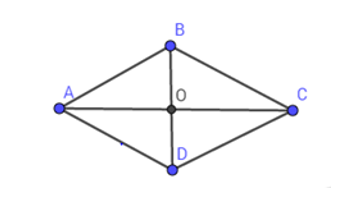
Áp dụng định lí Py-ta-go trong tam giác vuông \(AOB\) vuông tại \(O\) ta có:
\(BO = \sqrt {A{B^2} - O{A^2}} = \sqrt {{{20}^2} - {{16}^2}} = 12\).
\({S_{ABCD}} = \dfrac{1}{2}BD.AC = \dfrac{1}{2}2. BO. 2AO\)\( = 2BO. AO = 2. 12. 16 = 384\left( {c{m^2}} \right)\).
Cho tứ giác \(ABCD\) có đường chéo \(AC\) vuông góc với \(BD\), diện tích của \(ABCD\) là \(56\,c{m^2};BD = 7cm\). Độ dài đường chéo \(AC\) là:
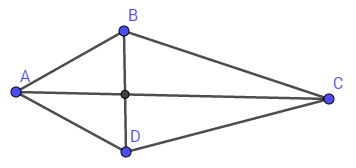
Vì \(ABCD\) có hai đường chéo vuông góc nên \({S_{ABCD}} = \dfrac{1}{2}BD.AC\)\( \Rightarrow AC = \dfrac{{2{S_{ABCD}}}}{{BD}} = \dfrac{{2. 56}}{7} = 16\,cm\).
Một hình thang có đáy nhỏ là \(11\,cm\), chiều cao là \(5\,cm\), diện tích là \(65\,c{m^2}\). Độ dài đáy lớn là:
Gọi đáy lớn của hình thang là \(a\left( {cm;a > 0} \right)\).
Diện tích hình thang \(S = \dfrac{{\left( {11 + a} \right)5}}{2} \Leftrightarrow \dfrac{{\left( {11 + a} \right)5}}{2} = 65\).
\( \Leftrightarrow 55 + 5a = 130 \Leftrightarrow 5a = 75 \Leftrightarrow a = 15\left( {tm} \right)\)
Vậy độ dài đáy lớn là \(15\,cm.\)
Cho hình vẽ dưới đây với \(ABCD\) là hình chữ nhật, \(MNBC\) là hình bình hành. Biết diện tích \(ABCD\) bằng \(25\,c{m^2},\) diện tích hình bình hành \(MNBC\) là:
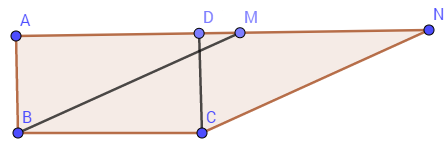
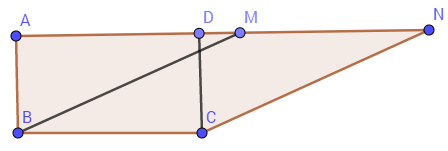
Vì ABCD là hình chữ nhật và BCNM là hình bình hành nên ta có:
\(\begin{array}{l}{S_{ABCD}} = BC.DC\\{S_{BCNM}} = MN.DC\end{array}\).
Mà \(BC = MN\) (do BCNM là hình bình hành), suy ra \({S_{ABCD}} = {S_{BCNM}}\).
Lại có: theo giả thiết \({S_{ABCD}} = 25c{m^2} \Rightarrow {S_{BCNM}} = 25\,c{m^2}.\)
Tính diện tích mảnh đất hình thang vuông \(ABCD\) có độ dài hai đáy \(AB = 9\,cm;\,DC = 13,5\,cm;\,\widehat A = \widehat D = 90^\circ \) ( hình vẽ), biết tam giác \(BEC\) vuông tại \(E\) và có diện tích bằng \(18\,c{m^2}\).
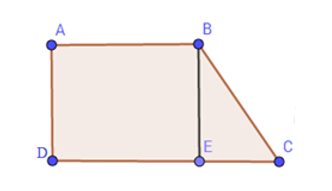
Tứ giác \(ABED\) có \(\widehat A = \widehat D = \widehat E = 90^\circ \) nên là hình chữ nhật.
Suy ra \(DE = AB = 9\,cm\). Do đó: \(EC = DC - DE = 13,5 - 9 = 4,5\,(cm)\)
Ta có:
\({S_{BEC}} = \dfrac{1}{2}BE.EC \Rightarrow BE = \dfrac{{2{S_{BEC}}}}{{EC}} = \dfrac{{2.18}}{{4,5}} = 8\,(cm)\).
\({S_{ABED}} = AB.BE = 9. 8 = 72\,\,\left( {c{m^2}} \right)\).
\({S_{ABCD}} = {S_{ABED}} + {S_{BEC}} = 72 + 18 = 90\,(c{m^2})\).
Hình thoi có độ dài hai đường chéo là \(15\,cm\) và \(20\,cm\). Tính độ dài đường cao của hình thoi.
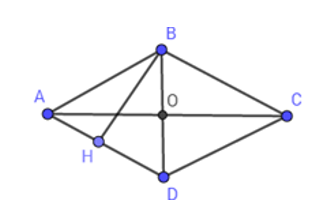
Giả sử hình thoi \(ABCD\), đường chéo \(AC\) vuông góc với \(BD\) tại \(O\), \(AC = 20\,cm;\,BD = 15\,cm\).
Gọi \(BH\) là đường cao hình thoi kẻ từ đỉnh \(B\).
Ta có: \(DO = \dfrac{1}{2}BD = \dfrac{1}{2}.15 = 7,5\,(cm);\,\)\(AO = \dfrac{1}{2}AC = \dfrac{1}{2}.20 = 10\,(cm)\).
Áp dụng định lí Py-ta-go trong tam giác vuông \(AOD\) vuông tại \(O\) ta có:
\(\begin{array}{l}AD = \sqrt {A{O^2} + O{D^2}} = \sqrt {{{10}^2} + 7,{5^2}} = 12,5\,(cm)\\{S_{ABCD}} = \dfrac{1}{2}BD.AC = \dfrac{1}{2}.15.20 = 150\left( {c{m^2}} \right)\\{S_{ABCD}} = BH.AD\\ \Rightarrow BH = \dfrac{{{S_{ABCD}}}}{{AD}} = \dfrac{{150}}{{12,5}} = 12\,(cm).\end{array}\).
Tính diện tích tứ giác \(EFGH\) theo \(S.\)
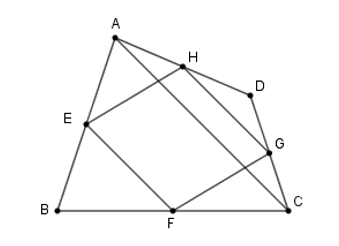
Theo kết quả câu trước ta có: \({S_{BEF}} = \dfrac{1}{4}{S_{ABC}}\).
Chứng minh tương tự ta có: \({S_{DHG}} = \dfrac{1}{4}{S_{DAC}};\,{S_{AEH}} = \dfrac{1}{4}{S_{ABD}};\,{S_{CDF}} = \dfrac{1}{4}{S_{CDB}}\).
Từ đó ta có: \({S_{BEF}} + {S_{DHG}} = \dfrac{1}{4}{S_{BAC}} + \dfrac{1}{4}{S_{DAC}}\)\( = \dfrac{1}{4}\left( {{S_{BAC}} + {S_{DAC}}} \right) = \dfrac{1}{4}{S_{ABCD}} = \dfrac{1}{4}S\).
Và \({S_{AEH}} + {S_{CGF}} = \dfrac{1}{4}{S_{BAD}} + \dfrac{1}{4}{S_{DBC}}\)\( = \dfrac{1}{4}\left( {{S_{BAD}} + {S_{DBC}}} \right) = \dfrac{1}{4}{S_{ABCD}} = \dfrac{1}{4}S\).
Suy ra: \({S_{AEH}} + {S_{CGF}} + {S_{BEF}} + {S_{CFG}} = \dfrac{1}{4}S + \dfrac{1}{4}S = \dfrac{1}{2}S\).
Từ đó: \({S_{EFGH}} = {S_{ABCD}} - \left( {{S_{AEH}} + {S_{CGF}} + {S_{BEF}} + {S_{CFG}}} \right) = S - \dfrac{1}{2}S = \dfrac{1}{2}S\).

