Trả lời bởi giáo viên
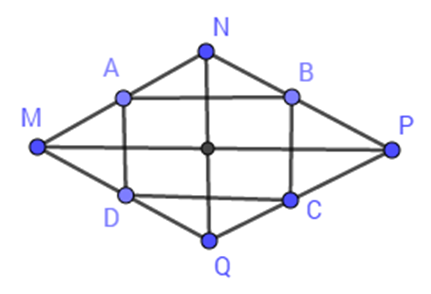
Xét tam giác $MNP$ có: \(MA = AN;\,NB = BP(gt) \Rightarrow \) $AB$ là đường trung bình của tam giác $MNP$ \( \Rightarrow AB = \dfrac{1}{2}MP;\,AB{\rm{//}}MP\,(1)\) (tính chất đường trung bình của tam giác).
Xét tam giác $MQP$ có: \(MD = DQ;\,PC = CQ(gt) \Rightarrow \) $CD$ là đường trung bình của tam giác $MQP$ \( \Rightarrow CD = \dfrac{1}{2}MP;\,CD{\rm{//}}MP\,(2)\) (tính chất đường trung bình của tam giác).
Xét tam giác $MNQ$ có: \(MA = AN;\,MD = DQ(gt) \Rightarrow \) $AD$ là đường trung bình của tam giác $MNQ$ \( \Rightarrow AD = \dfrac{1}{2}NQ;\,AD{\rm{//}}NQ\) (tính chất đường trung bình của tam giác).
Từ (1) và (2) suy ra \(AB = CD;AB{\rm{//}}CD \Rightarrow \) $ABCD$ là hình bình hành (dhnb).
Ta có: \(AB{\rm{//}}MP(cmt);\,NQ \bot MP(gt) \Rightarrow AB \bot NQ\) . Mặt khác \(AD{\rm{//}}NQ\,\,(cmt)\) , suy ra \(AD \bot AB \Rightarrow \widehat {DAB} = 90^\circ \)
Hình bình hành $ABCD$ có \(\widehat {DAB} = 90^\circ \) nên là hình chữ nhật (dhnb).
Diện tích hình thoi $MNPQ$ là: \({S_{MNPQ}} = \dfrac{1}{2}MP.NQ\,(3)\)
Diện tích hình chữ nhật $ABCD$ là: \({S_{ABCD}} = AB.AD = \dfrac{1}{2}MP.\dfrac{1}{2}NQ = \dfrac{1}{4}MP.NQ\,\,(4)\)
Từ (3) và (4) suy ra \(\dfrac{{{S_{ABCD}}}}{{{S_{MNPQ}}}} = \dfrac{1}{2}\) .
Hướng dẫn giải:
Chứng minh tứ giác $ABCD$ là hình chữ nhật, từ đó lập công thức tính diện tích hình chữ nhật$ABCD$ và lập công thức tính diện tích hình thoi$MNPQ$ sau đó lập tỉ số diện tích hai hình.

