Diện tích hình chữ nhật, diện tích tam giác

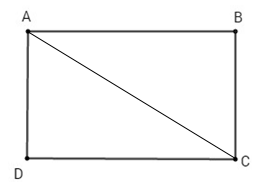
Vì $ABCD$ là hình chữ nhật nên ${S_{ABCD}} = AD.DC = AB.AD$ nên A sai, B đúng

Ta có: $\Delta ADC,\,\Delta ABC$ là các tam giác vuông nên ${S_{ADC}} = \dfrac{1}{2}AD.DC;\,{S_{ABC}} = \dfrac{1}{2}AB.BC$, do đó C, D sai.

Theo công thức tính diện tích hình chữ nhật $S = a.b$ thì diện tích hình chữ nhật tỉ lệ thuận với chiều dài và chiều rộng của nó

Nếu $a' = \dfrac{a}{6};\,\,\,b' = 3b;\,$ thì $S' = a'.b' = \dfrac{1}{6}a.3b = \dfrac{1}{2}ab = \dfrac{1}{2}S = \dfrac{1}{2}S$ .

Do đó diện tích mới giảm $2$ lần so với diện tích đã cho.

Theo công thức tính diện tích tam giác vuông có 2 cạnh góc vuông có độ dài $a,b$ là $S = \dfrac{1}{2}a.b$

Tam giác vuông mới có độ dài hai cạnh góc vuông $a',b'$ thì theo đề bài ta có  $a' = \dfrac{1}{3}a;\,\,\,b' = 3b;\,$

Khi đó, diện tích $S' = \dfrac{1}{2}a'.b' = \dfrac{1}{2}\dfrac{1}{3}a.3b = \dfrac{1}{2}ab = S$

Do đó diện tích hình tam giác mới không thay đổi so với tam giác ban đầu

Gọi $AH$ là đường cao ứng với cạnh $BC$. Theo công thức tính diện tích tam giác ta có $S = \dfrac{1}{2}AH.BC \Leftrightarrow \dfrac{1}{2}AH.6 = 24 \Leftrightarrow AH = 8\,cm$.

Từ công thức tính diện tích tam giác ta có ${S_{ABC}} = \dfrac{1}{2}AH.BC = \dfrac{1}{2}.5.8 = 20\,c{m^2}$.

Kẻ $AH \bot BC$ tại $H$. 

Mà $BM = 4CM$$\Rightarrow BM = \dfrac{4}{5}BC;\,CM = \dfrac{1}{5}BC;\,$

 Khi đó ta có:

 $\begin{array}{l}{S_{ABM}} = \dfrac{1}{2}.\,AH.BM = \dfrac{1}{2}AH.\dfrac{4}{5}BC\\ = \dfrac{4}{5}.\left( {\dfrac{1}{2}AH.BC} \right) = \dfrac{4}{5}{S_{ABC}}\end{array}$

Suy ra A sai.

 $\begin{array}{l}{S_{AMB}} = \dfrac{1}{2}.\,AH.MB = \dfrac{1}{2}AH.4MC\\ = 4.\left( {\dfrac{1}{2}AH.MC} \right) = 4{S_{AMC}}\end{array}$

Suy ra B sai.

 ${S_{ABC}} = \dfrac{1}{2}.\,AH.BC = \dfrac{1}{2}AH.5MC = 5{S_{AMC}}$

 suy ra C đúng, D sai.

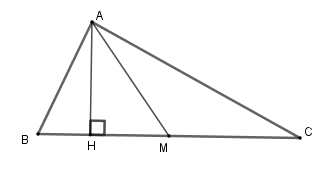
Kẻ $AH \bot BC$ tại $H$. 

Ta có ${S_{ABC}} = \dfrac{1}{2}AH.BC;\,{S_{AMC}} = \dfrac{1}{2}AH.MC$

Mà $AM$ là đường trung tuyến nên $M$ là trung điểm của $BC$$\Rightarrow BC = 2AM$

Từ đó ${S_{ABC}} = \dfrac{1}{2}AH.BC = \dfrac{1}{2}AH.2MC = 2{S_{AMC}}$

Suy ra ${S_{AMC}} = \dfrac{1}{2}{S_{ABC}} = \dfrac{1}{2}.40 = 20\,c{m^2}$.

Vậy ${S_{AMC}} = 20\,c{m^2}$ .

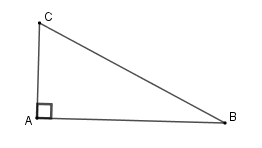
Áp dụng định lý Pytago cho tam giác vuông $ABC$ ta có

 $\begin{array}{l}B{C^2} = A{C^2} + A{B^2}\\ \Rightarrow A{B^2} = {13^2} - {5^2}\\ \Rightarrow A{B^2} = 144 \Rightarrow AB = 12\,cm\end{array}$

Suy ra ${S_{ABC}} = \dfrac{{AC.AB}}{2} = \dfrac{{5.12}}{2} = 30\,c{m^2}$.

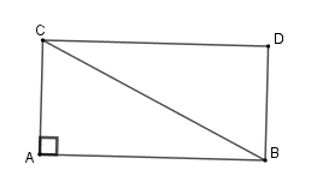
Vì $ABDC$ là hình chữ nhật nên ${S_{ABDC}} = AC.AB$ mà ${S_{ABC}} = \dfrac{{AC.AB}}{2}$

Nên ${S_{ABDC}} = 2{S_{ABC}} = 2.55 = 110\,c{m^2}$.

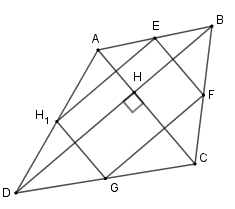
+ Vì $E,F,G,H$ lần lượt là trung điểm các cạnh$AB,BC,CD,DA$ nên $EF;\,FG;\,GH;\,HE$ lần lượt là đường trung bình của các tam giác $ABC;\,BCD;\,ADC;\,ADB$

nên $EF{\rm{//}}HG$ (vì cùng song song với $AC$ ); $HE{\rm{//}}FG\,$( vì cùng song song với $BD$ )

Suy ra tứ giác $EFGH$ là hình bình hành, mà $AC \bot BD\,\left( {gt} \right) \Rightarrow EFGH$ là hình chữ nhật.

Do đó ${S_{EFGH}} = HE.EF$, mà $EF = \dfrac{1}{2}AC; \,HE = \dfrac{1}{2}BD$ (tính chất đường trung bình)

Nên ${S_{EFGH}} = \dfrac{1}{2}AC.\dfrac{1}{2}BD = \dfrac{1}{4}AC.BD$.

+ Gọi $H$ là giao của $AC$ và $BD$.

Khi đó

 $\begin{array}{l}{S_{ABCD}} = {S_{ABC}} + {S_{ACD}}\\ = \dfrac{1}{2}BH.AC + \dfrac{1}{2}DH.AC\\ = \dfrac{1}{2}AC\left( {BH + DH} \right)\\ = \dfrac{1}{2}AC.BD\end{array}$

Mà ${S_{ABCD}} = 40\,{m^2} \Rightarrow \dfrac{1}{2}AC.BD = 40 \Rightarrow AC.BD = 80\,{m^2}$.

Suy ra ${S_{EFGH}} = \dfrac{1}{4}AC.BD = \dfrac{1}{4}.80 = 20\,{m^2}$.

Gọi chiều rộng hình chữ nhật là $a$, ta có: $S = a.15 \Leftrightarrow 15.a = 120 \Leftrightarrow a = 8\,cm$.

Chu vi hình chữ nhật là $P = \left( {15 + 8} \right).2 = 46\,cm$.

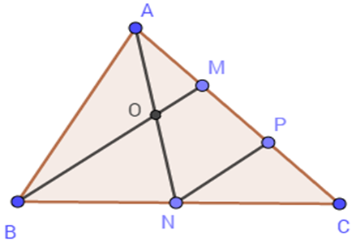
+ Lấy $P$ là trung điểm của$CM$ .

Tam giác BCM có: $\left\{ \begin{array}{l}NB = NC\,\,(gt)\\PC = PM\,\,(gt)\end{array} \right.$

Suy ra $NP$ là đường trung bình của tam giác $BMC$ (định nghĩa).

Suy ra $NP{\rm{//}}BM$  (tính chất đường trung bình).

Tam giác $ANP$ có  $\left\{ \begin{array}{l}MA = MP\,\,\,(gt)\\OM{\rm{//}}NP\,\,\,({\rm{do}}\,\,NP{\rm{//}}BM)\end{array} \right.$

$\Rightarrow AO = ON$ (định lý đảo của đường trung bình) .

+ Ta có $OM$ là đường trung bình của tam giác $ANP$ (cmt) nên $OM = \dfrac{1}{2}NP\,\,\,\,(1)$

$NP$ là đường trung bình của tam giác $BCM$ nên $NP = \dfrac{1}{2}BM\,\,\,(2)$

Từ (1) và (2) suy ra $BM = 4OM \Rightarrow BO = 3OM$ .

Vậy $AO = ON;\,BO = 3OM$ .

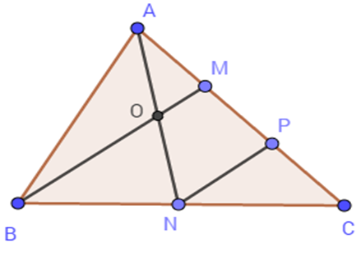
Hai tam giác $AOM$ và $ABM$ có chung đường cao hạ từ $A$ nên  $\dfrac{{{S_{AOM}}}}{{{S_{ABM}}}} = \dfrac{{OM}}{{BM}} = \dfrac{1}{4} \Rightarrow {S_{AOM}} = \dfrac{1}{4}{S_{ABM}}$

Hai tam giác $ABM$ và $ABC$ có chung đường cao hạ từ $B$ nên $\dfrac{{{S_{ABM}}}}{{{S_{ABC}}}} = \dfrac{{AM}}{{AC}} = \dfrac{1}{3} \Rightarrow {S_{ABM}} = \dfrac{1}{3}{S_{ABC}}$

Vậy ${S_{AOM}} = \dfrac{1}{4}.\dfrac{1}{3}.12 = 1\left( {c{m^2}} \right)$

+ Lấy $P$ là trung điểm của$CM$ .

Tam giác BCM có: $\left\{ \begin{array}{l}NB = NC\,\,(gt)\\PC = PM\,\,(gt)\end{array} \right.$

Suy ra $NP$ là đường trung bình của tam giác $BMC$ (định nghĩa).

Suy ra $NP{\rm{//}}BM$  (tính chất đường trung bình).

Tam giác $ANP$ có  $\left\{ \begin{array}{l}MA = MP\,\,\,(gt)\\OM{\rm{//}}NP\,\,\,({\rm{do}}\,\,NP{\rm{//}}BM)\end{array} \right.$

$\Rightarrow AO = ON$ (định lý đảo của đường trung bình) .

+ Ta có $OM$ là đường trung bình của tam giác $ANP$ (cmt) nên $OM = \dfrac{1}{2}NP\,\,\,\,(1)$

$NP$ là đường trung bình của tam giác $BCM$ nên $NP = \dfrac{1}{2}BM\,\,\,(2)$

Từ (1) và (2) suy ra $BM = 4OM \Rightarrow BO = 3OM$ .

Vậy $AO = ON;\,BO = 3OM$ .

+ Lấy $P$ là trung điểm của$CM$ .

Tam giác BCM có: $\left\{ \begin{array}{l}NB = NC\,\,(gt)\\PC = PM\,\,(gt)\end{array} \right.$

Suy ra $NP$ là đường trung bình của tam giác $BMC$ (định nghĩa).

Suy ra $NP{\rm{//}}BM$  (tính chất đường trung bình).

Tam giác $ANP$ có  $\left\{ \begin{array}{l}MA = MP\,\,\,(gt)\\OM{\rm{//}}NP\,\,\,({\rm{do}}\,\,NP{\rm{//}}BM)\end{array} \right.$

$\Rightarrow AO = ON$ (định lý đảo của đường trung bình) .

+ Ta có $OM$ là đường trung bình của tam giác $ANP$ (cmt) nên $OM = \dfrac{1}{2}NP\,\,\,\,(1)$

$NP$ là đường trung bình của tam giác $BCM$ nên $NP = \dfrac{1}{2}BM\,\,\,(2)$

Từ (1) và (2) suy ra $BM = 4OM \Rightarrow BO = 3OM$ .

Vậy $AO = ON;\,BO = 3OM$ .

+ Diện tích hình chữ nhật bằng tích hai kích thước của nó: $S = a.b$ .

+ Diện tích vuông bằng bình phương cạnh của nó: $S = {a^2}$ .

+ Diện tích tam giác vuông bằng nửa tích hai cạnh góc vuông nên A đúng.

Theo công thức tính diện tích hình chữ nhật $S = a.b$ thì diện tích hình chữ nhật tỉ lệ thuận với chiều dài và chiều rộng của nó

Nếu $a' = 4a;\,\,\,b' = \dfrac{1}{2}b;\,$ thì $S' = a'.b' = 4a.\dfrac{1}{2}b = \dfrac{4}{2}ab = \dfrac{4}{2}S = 2S.$ 

Do đó diện tích tăng $2$ lần so với diện tích đã cho.

Gọi $a;b$ lần lượt là chiều dài và chều rộng của hình chữ nhật ban đầu.

Diện tích hình chữ nhật ban đầu là $S=a.b$

Nếu giảm chiều dài đi 5 lần thì chiều dài mới là $a' = \dfrac{1}{5}a$

Nếu tăng chiều rộng 5 lần thì chiều rộng mới là $b' = 5b$ 

Lúc này, diện tích của hình chữ nhật mới là $S' = a'.b' = \dfrac{1}{5}a.5b = ab = S$

Do đó diện tích hình chữ nhật không thay đổi.

Gọi $AH$ là đường cao ứng với cạnh $BC$ . Theo công thức tính diện tích tam giác ta có $S = \dfrac{1}{2}AH.BC \Leftrightarrow \dfrac{1}{2}AH.8 = 16 \Leftrightarrow AH = 4\,cm$ .

Từ công thức tính diện tích tam giác ta có ${S_{ABC}} = \dfrac{1}{2}AH.BC = \dfrac{1}{2}.9.12 = 54\,c{m^2}$ .