Cho tứ giác \(ABCD\) có hai đường chéo vuông góc với nhau. Gọi \(E,F,G,H\) lần lượt là trung điểm các cạnh \(AB,BC,CD,DA\). Biết diện tích của tứ giác \(ABCD\) là \(40\,{m^2}\) thì diện tích của tứ giác \(EFGH\) là:

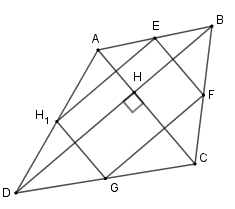
+ Vì \(E,F,G,H\) lần lượt là trung điểm các cạnh\(AB,BC,CD,DA\) nên \(EF;\,FG;\,GH;\,HE\) lần lượt là đường trung bình của các tam giác \(ABC;\,BCD;\,ADC;\,ADB\)

nên \(EF{\rm{//}}HG\) (vì cùng song song với \(AC\) ); \(HE{\rm{//}}FG\,\)( vì cùng song song với \(BD\) )

Suy ra tứ giác \(EFGH\) là hình bình hành, mà \(AC \bot BD\,\left( {gt} \right) \Rightarrow EFGH\) là hình chữ nhật.

Do đó \({S_{EFGH}} = HE.EF\), mà \(EF = \dfrac{1}{2}AC; \,HE = \dfrac{1}{2}BD\) (tính chất đường trung bình)

Nên \({S_{EFGH}} = \dfrac{1}{2}AC.\dfrac{1}{2}BD = \dfrac{1}{4}AC.BD\).

+ Gọi \(H\) là giao của \(AC\) và \(BD\).

Khi đó

 \(\begin{array}{l}{S_{ABCD}} = {S_{ABC}} + {S_{ACD}}\\ = \dfrac{1}{2}BH.AC + \dfrac{1}{2}DH.AC\\ = \dfrac{1}{2}AC\left( {BH + DH} \right)\\ = \dfrac{1}{2}AC.BD\end{array}\)

Mà \({S_{ABCD}} = 40\,{m^2} \Rightarrow \dfrac{1}{2}AC.BD = 40 \Rightarrow AC.BD = 80\,{m^2}\).

Suy ra \({S_{EFGH}} = \dfrac{1}{4}AC.BD = \dfrac{1}{4}.80 = 20\,{m^2}\).