Câu hỏi:
2 năm trước
Cho tam giác \(ABC\), \(AM\) là đường trung tuyến. Biết diện tích của \(\Delta ABC\) bằng \(40\,c{m^2}\). Diện tích của tam giác \(AMC\) là:
Trả lời bởi giáo viên
Đáp án đúng: c
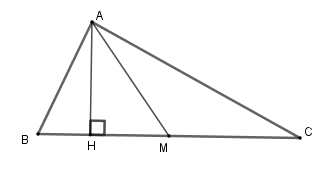
Kẻ \(AH \bot BC\) tại \(H\).
Ta có \({S_{ABC}} = \dfrac{1}{2}AH.BC;\,{S_{AMC}} = \dfrac{1}{2}AH.MC\)
Mà \(AM\) là đường trung tuyến nên \(M\) là trung điểm của \(BC\)\( \Rightarrow BC = 2AM\)
Từ đó \({S_{ABC}} = \dfrac{1}{2}AH.BC = \dfrac{1}{2}AH.2MC = 2{S_{AMC}}\)
Suy ra \({S_{AMC}} = \dfrac{1}{2}{S_{ABC}} = \dfrac{1}{2}.40 = 20\,c{m^2}\).
Vậy \({S_{AMC}} = 20\,c{m^2}\) .
Hướng dẫn giải:
Bước 1: Sử dụng công thức: Diện tích tam giác bằng nửa tích một cạnh với chiều cao ứng với cạnh đó: \(S = \dfrac{1}{2}ah\)
Bước 2: Dựa vào dữ kiện \(M\) là trung điểm của \(BC\) ta tìm được mối quan hệ diện tích giữa \(\Delta ABC\) và \(\Delta AMC\) và suy ra diện tích \(\Delta AMC\).
