Câu hỏi:
3 năm trước
Cho tam giác \(ABC\) vuông tại \(A\), biết \(BC = 13\,cm;AC = 5cm\). Diện tích tam giác \(ABC\) là:
Trả lời bởi giáo viên
Đáp án đúng: a
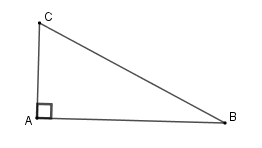
Áp dụng định lý Pytago cho tam giác vuông \(ABC\) ta có
\(\begin{array}{l}B{C^2} = A{C^2} + A{B^2}\\ \Rightarrow A{B^2} = {13^2} - {5^2}\\ \Rightarrow A{B^2} = 144 \Rightarrow AB = 12\,cm\end{array}\)
Suy ra \({S_{ABC}} = \dfrac{{AC.AB}}{2} = \dfrac{{5.12}}{2} = 30\,c{m^2}\).
Hướng dẫn giải:
+ Bước 1: Tính cạnh \(AB\) dựa vào định lý Pytago.
+ Bước 2: Sử dụng công thức: Diện tích tam giác vuông bằng nửa tích hai cạnh góc vuông: \(S = \dfrac{{ab}}{2}\).

