Tìm $x \in \mathbb{Z}$ để $P + 1 \in \mathbb{Z}$.
Theo câu trước ta có $P = \dfrac{{ - 3x + 7}}{{x + 4}}$ với \(x \ne 1;x \ne -4\), nên
$P + 1 = \dfrac{{ - 3x + 7}}{{x + 4}} + 1 = \dfrac{{ - 3x + 7 + x + 4}}{{x + 4}} = \dfrac{{ - 2x + 11}}{{x + 4}} = - 2 + \dfrac{{19}}{{x + 4}}$
$x \in Z$ để $P + 1 \in Z \Rightarrow \left( {x + 4} \right) \in U\left( {19} \right) = \left\{ { \pm 1;\, \pm 19} \right\}$
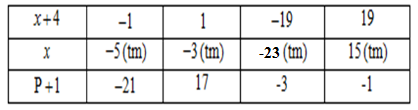
Vậy $x \in \left\{ { - 23; - 5; - 3;15} \right\}$ thì $P + 1 \in Z$.
Tính giá trị của $P$ khi $x = - 1.$
Theo câu trước ta có: $P = \dfrac{{ - 3x + 7}}{{x + 4}}$ với \(x \ne 1;x \ne -4\)
Khi $x = - 1(t/m) \Rightarrow P = \dfrac{{ - 3.( - 1) + 7}}{{ - 1 + 4}} = \dfrac{{10}}{3}$
Vậy khi $x = - 1$ thì $P = \dfrac{{10}}{3}.$
Rút gọn \(P\) ta được
ĐK: \(\left\{ \begin{array}{l}{x^2} + 3x - 4 \ne 0\\x + 4 \ne 0\\1 - x \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left( {x - 1} \right)\left( {x + 4} \right) \ne 0\\x \ne 1\\x \ne - 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ne 1\\x \ne - 4\end{array} \right..\)
$\begin{array}{l}P = \dfrac{{10x}}{{{x^2} + 3x - 4}} - \dfrac{{2x - 3}}{{x + 4}} + \dfrac{{x + 1}}{{1 - x}}\\ = \dfrac{{10x}}{{\left( {x - 1} \right)\left( {x + 4} \right)}} - \dfrac{{2x - 3}}{{x + 4}} - \dfrac{{x + 1}}{{x - 1}}\\ = \dfrac{{10x - (2x - 3)(x - 1) - (x + 1)(x + 4)}}{{(x - 1)(x + 4)}}\\ = \dfrac{{10x - 2{x^2} + 2x + 3x - 3 - {x^2} - 4x - x - 4}}{{(x - 1)(x + 4)}}\\ = \dfrac{{ - 3{x^2} + 10x - 7}}{{(x - 1)(x + 4)}}\\ = - \dfrac{{ - (x - 1)(3x - 7)}}{{(x - 1)(x + 4)}}\\ = \dfrac{{ - 3x + 7}}{{x + 4}}.\end{array}$
Vậy $P = \dfrac{{ - 3x + 7}}{{x + 4}}$ với \(x \ne 1;x \ne -4\)
Rút gọn \(P\) ta được
ĐK: \(\left\{ \begin{array}{l}{x^2} + 3x - 4 \ne 0\\x + 4 \ne 0\\1 - x \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left( {x - 1} \right)\left( {x + 4} \right) \ne 0\\x \ne 1\\x \ne - 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ne 1\\x \ne - 4\end{array} \right..\)
$\begin{array}{l}P = \dfrac{{10x}}{{{x^2} + 3x - 4}} - \dfrac{{2x - 3}}{{x + 4}} + \dfrac{{x + 1}}{{1 - x}}\\ = \dfrac{{10x}}{{\left( {x - 1} \right)\left( {x + 4} \right)}} - \dfrac{{2x - 3}}{{x + 4}} - \dfrac{{x + 1}}{{x - 1}}\\ = \dfrac{{10x - (2x - 3)(x - 1) - (x + 1)(x + 4)}}{{(x - 1)(x + 4)}}\\ = \dfrac{{10x - 2{x^2} + 2x + 3x - 3 - {x^2} - 4x - x - 4}}{{(x - 1)(x + 4)}}\\ = \dfrac{{ - 3{x^2} + 10x - 7}}{{(x - 1)(x + 4)}}\\ = - \dfrac{{ - (x - 1)(3x - 7)}}{{(x - 1)(x + 4)}}\\ = \dfrac{{ - 3x + 7}}{{x + 4}}.\end{array}$
Vậy $P = \dfrac{{ - 3x + 7}}{{x + 4}}$ với \(x \ne 1;x \ne -4\)
Phân thức $\dfrac{{5x - 7}}{{3{x^2} + 6x}}$ xác định khi:
ĐK: \(3{x^2} + 6x \ne 0 \Leftrightarrow 3x\left( {x + 2} \right) \ne 0 \Leftrightarrow \left\{ \begin{array}{l}
x \ne 0\\
x \ne - 2
\end{array} \right.\)
Đa thức thích hợp để điền vào chỗ trống trong đẳng thức \(\dfrac{{{x^3} - 8}}{{......}} = \dfrac{{{x^2} + 2x + 4}}{{3x}}\) là:
\(\begin{array}{l}\dfrac{{{x^2} + 2x + 4}}{{3x}} = \dfrac{{(x - 2)({x^2} + 2x + 4)}}{{3x(x - 2)}} = \dfrac{{{x^3} - 8}}{{3x(x - 2)}}\\ \Rightarrow \dfrac{{{x^3} - 8}}{{3x(x - 2)}} = \dfrac{{{x^3} - 8}}{{......}}\end{array}\)
Vậy đa thức cần tìm là \(3x(x - 2)\)
Đa thức P trong đẳng thức \(\dfrac{{5{{(y - x)}^2}}}{{5{x^2} - 5xy}} = \dfrac{{x - y}}{P}\) là:
Ta có: \(\dfrac{{5{{(y - x)}^2}}}{{5{x^2} - 5xy}} = \dfrac{{5{{(x - y)}^2}}}{{5x(x - y)}} = \dfrac{{x - y}}{x} \Rightarrow \dfrac{{x - y}}{x} = \dfrac{{x - y}}{P} \Rightarrow P = x.\)
Kết quả của phép tính $\dfrac{{3x - 1}}{{2xy}} - \dfrac{{5x -2}}{{2xy}}$ là:
$\dfrac{{3x - 1}}{{2xy}} - \dfrac{{5x - 2}}{{2xy}} = \dfrac{{3x - 1 - 5x + 2}}{{2xy}} = \dfrac{{ - 2x + 1}}{{2xy}}$.
Thực hiện phép tính sau: $\dfrac{{{x^3}}}{{{x^2} + 1}} + \dfrac{x}{{{x^2} + 1}}$
Ta có $\dfrac{{{x^3}}}{{{x^2} + 1}} + \dfrac{x}{{{x^2} + 1}} = \dfrac{{{x^3} + x}}{{{x^2} + 1}} = \dfrac{{x({x^2} + 1)}}{{{x^2} + 1}} = x.$
Thực hiện phép tính sau $\dfrac{{2x + 5}}{{5{x^2}{y^2}}} + \dfrac{8}{{5x{y^2}}} + \dfrac{{2x - 1}}{{{x^2}{y^2}}}$, ta được kết quả là:
$\dfrac{{2x + 5}}{{5{x^2}{y^2}}} + \dfrac{8}{{5x{y^2}}} + \dfrac{{2x - 1}}{{{x^2}{y^2}}} = \dfrac{{2x + 5 + 8x + 10x - 5}}{{5{x^2}{y^2}}} = \dfrac{{20x}}{{5{x^2}{y^2}}} = \dfrac{4}{{x{y^2}}}.$
Điền vào chỗ trống: $\dfrac{{2x - 6}}{{x + 3}} - .... = \dfrac{{x + 1}}{2}$.
Gọi phân thức cần điền là $P,$ khi đó
$P=\dfrac{{2x - 6}}{{x + 3}} - \dfrac{{x + 1}}{2}$$ = \dfrac{{2(2x - 6) - (x + 3)(x + 1)}}{{2(x + 3)}} $$= \dfrac{{4x - 12 - {x^2} - x - 3x - 3}}{{2(x + 3)}} $$= \dfrac{{ - {x^2} - 15}}{{2(x + 3)}}.$
Kết quả của phép tính $\dfrac{1}{x} + \dfrac{1}{{x(x + 1)}} + ... + \dfrac{1}{{(x + 9)(x + 10)}}$ là:
Ta có : $\dfrac{1}{x} + \dfrac{1}{{x(x + 1)}} + ... + \dfrac{1}{{(x + 9)(x + 10)}}$
$\begin{array}{l} = \dfrac{1}{x} + \dfrac{1}{x} - \dfrac{1}{{x + 1}} + \dfrac{1}{{x + 1}} - \dfrac{1}{{x + 2}}... + \dfrac{1}{{x + 9}} - \dfrac{1}{{x + 10}}\\ = \dfrac{1}{x} + \dfrac{1}{x} + 0 + ... + 0 - \dfrac{1}{{x + 10}}\\ = \dfrac{2}{x} - \dfrac{1}{{x + 10}}\\ = \dfrac{{2x + 20 - x}}{{x(x + 10)}} = \dfrac{{x + 20}}{{x(x + 10)}}.\end{array}$
Rút gọn biểu thức $\dfrac{1}{{x + 2}} + \dfrac{1}{{(x + 1)(x + 2)}} + \dfrac{1}{{(x + 1)(2x + 1)}}$ ta được
Điều kiện: $x \ne - 1;x \ne - 2;x \ne \dfrac{{ - 1}}{2}.$
$\begin{array}{l}\,\,\,\,\dfrac{1}{{x + 2}} + \dfrac{1}{{(x + 1)(x + 2)}} + \dfrac{1}{{(x + 1)(2x + 1)}}\\ = \dfrac{{(2x + 1)(x + 1) + 2x + 1 + x + 2}}{{(x + 1)(x + 2)(2x + 1)}}\\ = \dfrac{{2{x^2} + x + 2x + 1 + 2x + 1 + x + 2}}{{(x + 1)(x + 2)(2x + 1)}}\\ = \dfrac{{2{x^2} + 6x + 4}}{{(x + 1)(x + 2)(2x + 1)}}\\ = \dfrac{{2({x^2} + 3x + 2)}}{{(x + 1)(x + 2)(2x + 1)}}\\ = \dfrac{{2\left( {{x^2} + x + 2x + 2} \right)}}{{\left( {x + 1} \right)\left( {x + 2} \right)\left( {2x + 1} \right)}}\\ = \dfrac{{2\left[ {x\left( {x + 1} \right) + 2\left( {x + 1} \right)} \right]}}{{\left( {x + 1} \right)\left( {x + 2} \right)\left( {2x + 1} \right)}}\\= \dfrac{{2(x + 1)(x + 2)}}{{(x + 1)(x + 2)(2x + 1)}} = \dfrac{2}{{2x + 1}}.\end{array}$
Chọn câu đúng.
Điều kiện: $x \ne 1.$
$\begin{array}{l}\dfrac{{4{x^2} - 3x + 5}}{{{x^3} - 1}} - \dfrac{{1 - 2x}}{{{x^2} + x + 1}} - \dfrac{6}{{x - 1}}\\ = \dfrac{{4{x^2} - 3x + 5 - (1 - 2x)(x - 1) - 6({x^2} + x + 1)}}{{(x - 1)({x^2} + x + 1)}}\\ = \dfrac{{4{x^2} - 3x + 5 - x + 1 + 2{x^2} - 2x - 6{x^2} - 6x - 6}}{{(x - 1)({x^2} + x + 1)}}\\ = \dfrac{{ - 12x}}{{{x^3} - 1}}.\end{array}$
Tìm $P$ biết: $P + \dfrac{{4x - 12}}{{{x^3} - 3{x^2} - 4x + 12}} = \dfrac{3}{{x - 3}} - \dfrac{{{x^2}}}{{4 - {x^2}}}$
ĐK: $x \ne {\rm{\{ }} - 2;2;3\} $.
$\begin{array}{l}P + \dfrac{{4x - 12}}{{{x^3} - 3{x^2} - 4x + 12}} = \dfrac{3}{{x - 3}} - \dfrac{{{x^2}}}{{4 - {x^2}}}\\P = \dfrac{3}{{x - 3}} - \dfrac{{{x^2}}}{{4 - {x^2}}} - \dfrac{{4x - 12}}{{{x^3} - 3{x^2} - 4x + 12}}\\P = \dfrac{3}{{x - 3}} + \dfrac{{{x^2}}}{{(x - 2)(x + 2)}} - \dfrac{{4x - 12}}{{{x^2}(x - 3) - 4(x - 3)}}\\P = \dfrac{{3\left( {{x^2} - 4} \right)}}{{\left( {x - 3} \right)\left( {{x^2} - 4} \right)}} + \dfrac{{{x^2}\left( {x - 3} \right)}}{{\left( {x - 3} \right)\left( {{x^2} - 4} \right)}} - \dfrac{{4x - 12}}{{\left( {x - 3} \right)\left( {{x^2} - 4} \right)}}\end{array}$
$P = \dfrac{{3{x^2} - 12 + {x^3} - 3{x^2} - 4x + 12}}{{\left( {x - 3} \right)\left( {{x^2} - 4} \right)}}$
$\begin{array}{l}P = \dfrac{{{x^3} - 4x}}{{(x - 3)(x - 2)(x + 2)}}\\P = \dfrac{{x({x^2} - 4)}}{{(x - 3)(x - 2)(x + 2)}} = \dfrac{x}{{x - 3}}\end{array}$
Thực hiện phép tính \(\dfrac{{3x + 15}}{{{x^2} - 4}}\,\,:\,\,\dfrac{{x + 5}}{{x - 2}}\) ta được:
$\dfrac{{3x + 15}}{{{x^2} - 4}}\,\,:\,\,\dfrac{{x + 5}}{{x - 2}} = \dfrac{{3x + 15}}{{{x^2} - 4}}\, \cdot \,\dfrac{{x - 2}}{{x + 5}} = \dfrac{{3(x + 5)}}{{(x - 2)(x + 2)}}\, \cdot \,\dfrac{{x - 2}}{{x + 5}} = \dfrac{3}{{x + 2}}.$
Rút gọn biểu thức \(\dfrac{{{x^4} + 4{x^2} + 5}}{{5{x^3} + 5}}\,\, \cdot \,\,\dfrac{{2x}}{{{x^2} + 4}}\,\, \cdot \,\,\dfrac{{3{x^3} + 3}}{{{x^4} + 4{x^2} + 5}}\) ta được:
\(\dfrac{{{x^4} + 4{x^2} + 5}}{{5{x^3} + 5}}\,\, \cdot \,\,\dfrac{{2x}}{{{x^2} + 4}}\,\, \cdot \,\,\dfrac{{3{x^3} + 3}}{{{x^4} + 4{x^2} + 5}} = \dfrac{{{x^4} + 4{x^2} + 5}}{{5({x^3} + 1)}}\,\, \cdot \,\,\dfrac{{2x}}{{{x^2} + 4}}\,\, \cdot \,\,\dfrac{{3({x^3} + 1)}}{{{x^4} + 4{x^2} + 5}} = \dfrac{{6x}}{{5({x^2} + 4)}}.\)
Biểu thức \(P = \dfrac{{x - 1}}{{2 - x}}\,\,:\,\,\dfrac{{x - 1}}{{x + 2}}\,\, \cdot \,\,\dfrac{{x - 2}}{{4 - {x^2}}}\) có kết quả rút gọn là:
\(P = \dfrac{{x - 1}}{{2 - x}}\,\,:\,\,\dfrac{{x - 1}}{{x + 2}}\,\, \cdot \,\,\dfrac{{x - 2}}{{4 - {x^2}}} = \dfrac{{x - 1}}{{2 - x}}\,\, \cdot \,\,\dfrac{{x + 2}}{{x - 1}}\,\, \cdot \,\,\dfrac{{ - \left( {2 - x} \right)}}{{(x + 2)(2 - x)}} = \dfrac{{ - 1}}{{2 - x}} = \dfrac{1}{{x - 2}}\)
Tìm biểu thức Q, biết: \(\dfrac{{5x}}{{{x^2} + 2x + 1}}\,\, \cdot \,\,Q = \dfrac{x}{{{x^2} - 1}}\)
\(\begin{array}{l}\dfrac{{5x}}{{{x^2} + 2x + 1}}\,\, \cdot \,\,Q = \dfrac{x}{{{x^2} - 1}}\\ \Rightarrow Q = \dfrac{x}{{{x^2} - 1}}:\dfrac{{5x}}{{{x^2} + 2x + 1}} \\= \dfrac{x}{{{x^2} - 1}} \cdot \dfrac{{{x^2} + 2x + 1}}{{5x}} \\= \dfrac{x}{{(x - 1)(x + 1)}} \cdot \dfrac{{{{(x + 1)}^2}}}{{5x}} \\= \dfrac{{x + 1}}{{5(x - 1)}}\end{array}\)
Tìm x, biết: \(\dfrac{1}{x} \cdot \dfrac{x}{{x + 1}} \cdot \dfrac{{x + 1}}{{x + 2}} \cdot \dfrac{{x + 2}}{{x + 3}} \cdot \dfrac{{x + 3}}{{x + 4}} \cdot \dfrac{{x + 4}}{{x + 5}} \cdot \dfrac{{x + 5}}{{x + 6}} = 1\)
Điều kiện: \(x \ne \left\{ {0; - 1; - 2; - 3; - 4; - 5; - 6} \right\}\)
\(\begin{array}{l}\dfrac{1}{x} \cdot \dfrac{x}{{x + 1}} \cdot \dfrac{{x + 1}}{{x + 2}} \cdot \dfrac{{x + 2}}{{x + 3}} \cdot \dfrac{{x + 3}}{{x + 4}} \cdot \dfrac{{x + 4}}{{x + 5}} \cdot \dfrac{{x + 5}}{{x + 6}} = 1\\ \Leftrightarrow \dfrac{1}{{x + 6}} = 1\\ \Rightarrow x + 6 = 1\\ \Leftrightarrow x = - 5 \, (KTM)\end{array}\)
Vậy phương trình vô nghiệm.

