Phép chia đa thức \(\left( {4{x^4} + 3{x^2} - 2x + 1} \right)\) cho đa thức \({x^2} + 1\) được đa thức dư là:
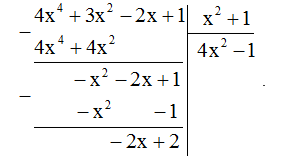
Vậy đa thức dư là \(R = - 2x + 2\) .
Điền vào chỗ trống: \(\left( {{x^3} + {x^2} - 12} \right):\left( {x - 2} \right) = .....\)

Vậy đa thức cần điền vào chỗ trống là \({x^2} + 3x + 6\).
Thương của phép chia đa thức \(\left( {3{x^4} - 2{x^3} + 4x - 2{x^2} - 8} \right)\) cho đa thức \(\left( {{x^2} - 2} \right)\) có hệ số tự do là
Ta có: \(\left( {3{x^4} - 2{x^3} + 4x - 2{x^2} - 8} \right):\left( {{x^2} - 2} \right) \)\(= \left( {3{x^4} - 2{x^3} - 2{x^2} + 4x - 8} \right):\left( {{x^2} - 2} \right)\)
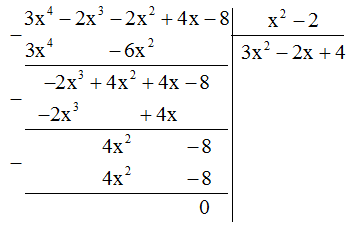
\(\left( {3{x^4} - 2{x^3} + 4x - 2{x^2} - 8} \right):\left( {{x^2} - 2} \right) = 3{x^2} - 2x + 4\)
Hệ số tự do của thương là \(4.\)
Thương và phần dư của phép chia đa thức \(2{x^3} - 3{x^2} - 3x - 2\) cho đa thức \({x^2} + 1\) lần lượt là
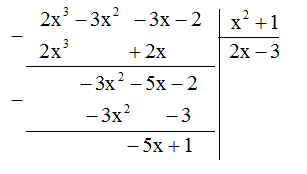
Thương của phép chia là \(2x - 3\) và dư là \( - 5x + 1\)
Cho các khẳng định sau:
(I): Phép chia đa thức \(\left( {2{x^3} - 26x - 24} \right)\) cho đa thức \({x^2} + 4x + 3\) là phép chia hết.
(II): Phép chia đa thức \(\left( {{x^3} - 7x + 6} \right)\) cho đa thức \(x + 3\) là phép chia hết.
Chọn câu đúng.
Ta có
\(\;\left( {2{x^3} - 26x - 24} \right):\left( {{x^2} + 4x + 3} \right)\)
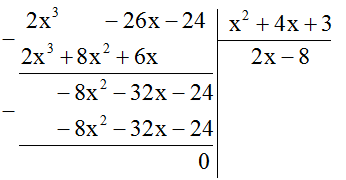
Vì phần dư \(R = 0\) nên phép chia đa thức \(\left( {2{x^3} - 26x - 24} \right)\)cho đa thức \({x^2} + 4x + 3\) là phép chia hết.
Do đó (I) đúng.
Lại có
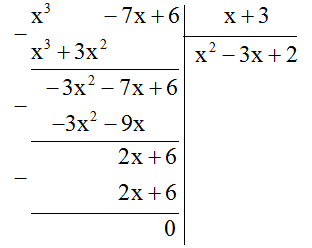
Nhận thấy phần dư \(R = 0\) nên phép chia đa thức \(\left( {{x^3} - 7x + 6} \right)\) cho đa thức \(x + 3\) là phép chia hết. Do đó (II) đúng.
Kết quả của phép chia \(({x^4} - {x^3}y + {x^2}{y^2} - x{y^3}):({x^2} + {y^2})\) là
Ta có \(({x^4} - {x^3}y + {x^2}{y^2} - x{y^3})\)
\( = {x^4} + {x^2}{y^2} - \left( {{x^3}y + x{y^3}} \right) \)\(= {x^2}\left( {{x^2} + {y^2}} \right) - xy\left( {{x^2} + {y^2}} \right)\)\( = \left( {{x^2} + {y^2}} \right)\left( {{x^2} - xy} \right) \)\(= \left( {{x^2} + {y^2}} \right)x\left( {x - y} \right)\)
Nên \(({x^4} - {x^3}y + {x^2}{y^2} - x{y^3}):({x^2} + {y^2})\)\(=x\left( {x - y} \right)\left( {{x^2} + {y^2}} \right):\left( {{x^2} + {y^2}} \right) = x\left( {x - y} \right)\) .
Xác định \(a\) để đa thức \(10{x^2} - 7x + a\) chia hết cho \(2x - 3\)
\(\left( {10{x^2} - 7x + a} \right) \vdots \left( {2x - 3} \right)\)
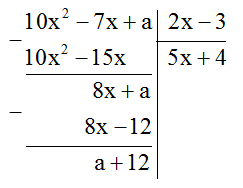
Để \(10{x^2} - 7x + a\) chia hết cho \(2x - 3\) thì \(a + 12 = 0 \Leftrightarrow a = - 12\)
Để đa thức \({x^3} + a{x^2} - 4\) chia hết cho \({x^2} + 4x + 4\) thì giá trị của \(a\) là
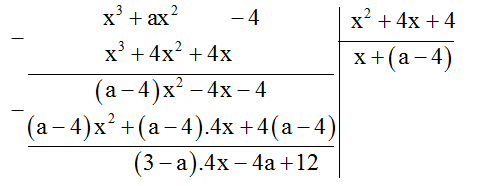
Để \({x^3} + a{x^2}-4\) chia hết cho \({x^2} + 4x + 4\) thì \(4\left( {3-a} \right).x-4a + 12 = 0\\ \Leftrightarrow \left\{ \begin{array}{l}4\left( {3 - a} \right) = 0\\12 - 4a = 0\end{array} \right.\\ \Leftrightarrow a = 3\).
Vậy \(a = 3\).
Tìm giá trị của \(a\) và \(b\) để đa thức \(4{x^3} + ax + b\) chia cho đa thức \({x^2} - 1\) dư \(2x - 3.\)
Ta có
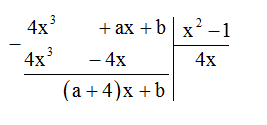
Phần dư của phép chia trên là \(R = \left( {a + 4} \right)x + b\) . Theo bài ra ta có \(\left( {a + 4} \right)x + b = 2x - 3 \Leftrightarrow \left\{ \begin{array}{l}a + 4 = 2\\b = - 3\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}a = - 2\\b = - 3\end{array} \right.\)
Vậy có hai giá trị của \(a\) thỏa mãn điều kiện đề bài \(a = - 2;b = - 3\) .
Xác định hằng số \(a\) và \(b\) sao cho \(\left( {{x^4} + ax + b} \right) \vdots \left( {{x^2} - 4} \right)\):
Ta có
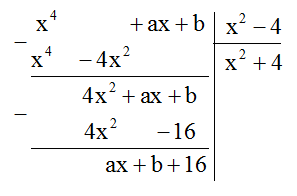
Để \({x^4} + ax + b\) chia hết cho \({x^2} - 4\) thì \(ax + b + 16 = 0 \Leftrightarrow \left\{ \begin{array}{l}ax = 0\\b + 16 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 0\\b = - 16\end{array} \right.\)
Phép chia đa thức \(2{x^4} - 3{x^3} + 3x - 2\) cho đa thức \({x^2} - 1\) được đa thức dư là:

Vậy đa thức dư là \(R = 0\) .
Phép chia đa thức \(3{x^5} + 5{x^4} - 1\) cho đa thức \({x^2} + x + 1\) được đa thức thương là:

Đa thức thương là $3{x^3} + 2{x^2} - 5x + 3$ .
Phần dư của phép chia đa thức \({x^4} - 2{x^3} + {x^2} - 3x + 1\) cho đa thức \({x^2} + 1\) có hệ số tự do là

Đa thức dư là \( - x + 1\) có hệ số tự do là \(1\) .
Biết phần dư của phép chia đa thức \(\left( {{x^5} + {x^3} + {x^2} + 2} \right)\) cho đa thức \(\left( {{x^3} + 1} \right)\) là số tự nhiên \(a\) . Chọn câu đúng.

Phần dư của phép chia là \(a = 1 < 2\)
Cho các khẳng định sau:
(I): Phép chia đa thức \(3{x^3} - 2{x^2} + 5\) cho đa thức \(3x - 2\) là phép chia hết.
(II): Phép chia đa thức \(\left( {2{x^3} + 5{x^2} - 2x + 3} \right)\) cho đa thức \(\left( {2{x^2} - x + 1} \right)\) là phép chia hết
Chọn câu đúng.
Ta có
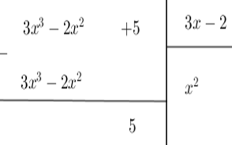
Vì phần dư \(R = 5 \ne 0\) nên phép chia đa thức \(3{x^3} - 2{x^2} + 5\) cho đa thức \(3x - 2\) là phép chia có dư. Do đó (I) sai.
Lại có

Nhận thấy phần dư \(R = 0\) nên phép chia đa thức \(\left( {2{x^3} + 5{x^2} - 2x + 3} \right)\) cho đa thức \(\left( {2{x^2} - x + 1} \right)\) là phép chia hết. Do đó (II) đúng.
Kết quả của phép chia \(\left( {2{a^3} + 7a{b^2} - 7{a^2}b - 2{b^3}} \right):\left( {2a - b} \right)\) là
Ta có \(2{a^3} + 7a{b^2} - 7{a^2}b - 2{b^3}\)\( = 2\left( {{a^3} - {b^3}} \right) - 7ab\left( {a - b} \right) \)\(= 2\left( {a - b} \right)\left( {{a^2} + ab + {b^2}} \right) - 7ab\left( {a - b} \right)\)
\( = \left( {a - b} \right)\left( {2{a^2} - ab - 4ab + 2{b^2}} \right) = \left( {a - b} \right)\left[ {a\left( {2a - b} \right) - 2b\left( {2a - b} \right)} \right]\)
\( = \left( {a - b} \right)\left( {2a - b} \right)\left( {a - 2b} \right)\)
Nên \(\left( {2{a^3} + 7a{b^2} - 7{a^2}b - 2{b^3}} \right):\left( {2a - b} \right)\)\( = {\left( {a - b} \right)}.(2a-b).\left( {a - 2b} \right):\left( {2a - b} \right) = \left( {a - b} \right)(a-2b)\) .
Tìm đa thức bị chia biết đa thức chia là \(\left( {{x^2} + x + 1} \right)\), thương là \(\left( {x + 3} \right)\), dư là \(x - 2\):
Đa thức bị chia cần tìm là:
\(\left( {{x^2} + x + 1} \right)\left( {x + 3} \right) + x - 2 = {x^2}.x + 3{x^2} + x.x + 3x + x + 3 + x - 2 = {x^3} + 4{x^2} + 5x + 1\)
Rút gọn và tính giá trị biểu thức \(A = \left( {4{x^3} + 3{x^2} - 2x} \right):\left( {{x^2} + \dfrac{3}{4}x - \dfrac{1}{2}} \right)\) tại \(x = 3\)
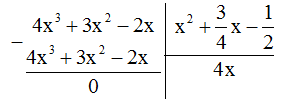
Tại \(x = 3\) , ta có: \(A = 4x = 4.3 = 12\)
Xác định \(a\) để đa thức \(27{x^2} + a\) chia hết cho \(3x + 2\)
Ta có
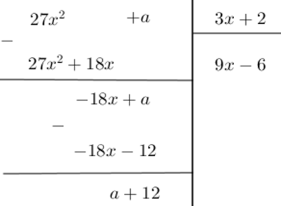
Suy ra \(27{x^2} + a = \left( {3x + 2} \right)\left( {9x - 6} \right) + a + 12\). Để phép chia trên là phép chia hết thì \(R = a + 12 = 0 \Leftrightarrow a = - 12\) .
Để đa thức \({x^4} + a{x^2} + 1\) chia hết cho \({x^2} + 2x + 1\) thì giá trị của \(a\) là
Ta có

Phần dư của phép chia đa thức \({x^4} + a{x^2} + 1\) chia hết cho\({x^2} + 2x + 1\) là \(R = \left( { - 2a - 4} \right)x - a - 2\) .
Để phép chia trên là phép chia hết thì \(R = 0 \Leftrightarrow \left( { - 2a - 4} \right)x - a - 2 = 0\) với mọi $x$
\( \Leftrightarrow \left\{ \begin{array}{l} - 2a - 4 = 0\\ - a - 2 = 0\end{array} \right. \Leftrightarrow a = - 2\) .

