Câu hỏi:
3 năm trước
Tìm giá trị của \(a\) và \(b\) để đa thức \(4{x^3} + ax + b\) chia cho đa thức \({x^2} - 1\) dư \(2x - 3.\)
Trả lời bởi giáo viên
Đáp án đúng: d
Ta có
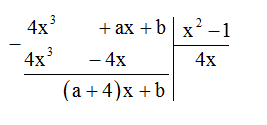
Phần dư của phép chia trên là \(R = \left( {a + 4} \right)x + b\) . Theo bài ra ta có \(\left( {a + 4} \right)x + b = 2x - 3 \Leftrightarrow \left\{ \begin{array}{l}a + 4 = 2\\b = - 3\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}a = - 2\\b = - 3\end{array} \right.\)
Vậy có hai giá trị của \(a\) thỏa mãn điều kiện đề bài \(a = - 2;b = - 3\) .
Hướng dẫn giải:
+ Sử dụng cách chia đa thức một biến đã sắp xếp.
+ Đồng nhất hệ số của đa thức dư tìm được và đa thức dư theo giả thiết ta tìm được \(a,b\)

