Cho các khẳng định sau:
(I): Phép chia đa thức \(\left( {2{x^3} - 26x - 24} \right)\) cho đa thức \({x^2} + 4x + 3\) là phép chia hết.
(II): Phép chia đa thức \(\left( {{x^3} - 7x + 6} \right)\) cho đa thức \(x + 3\) là phép chia hết.
Chọn câu đúng.
Trả lời bởi giáo viên
Ta có
\(\;\left( {2{x^3} - 26x - 24} \right):\left( {{x^2} + 4x + 3} \right)\)
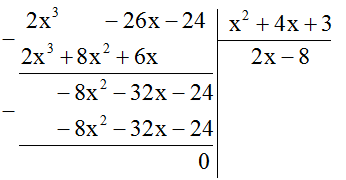
Vì phần dư \(R = 0\) nên phép chia đa thức \(\left( {2{x^3} - 26x - 24} \right)\)cho đa thức \({x^2} + 4x + 3\) là phép chia hết.
Do đó (I) đúng.
Lại có
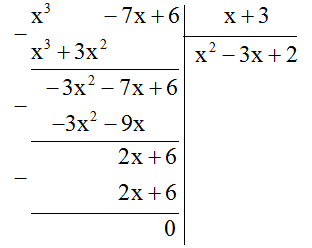
Nhận thấy phần dư \(R = 0\) nên phép chia đa thức \(\left( {{x^3} - 7x + 6} \right)\) cho đa thức \(x + 3\) là phép chia hết. Do đó (II) đúng.
Hướng dẫn giải:
- Đặt phép chia.
- Chia hạng tử bậc cao nhất của đa thức bị chia cho hạng tử bậc cao nhất của đa thức chia.
- Nhân kết quả tìm được với đa thức chia, rồi lấy đa thức bị chia trừ đi tích nhận được, hiệu tìm được gọi là dư thứ nhất.
- Chia hạng tử bậc cao nhất của dư thứ nhất cho hạng tử bậc cao nhất của đa thức chia, được kết quả lại thực hiện tương tự như trên, cho đến khi dư cuối cùng không thể chia được nữa.

