Có bao nhiêu giá trị của \(a\) để đa thức ${a^2}{x^3} + 3a{x^2}-6x-2a$ chia hết cho đa thức $x + 1$ .
Ta có

Phần dư của phép chia trên là \(R = - {a^2} + a + 6\) . Để phép chia trên là phép chia hết thì \(R = 0 \Leftrightarrow - {a^2} + a + 6 = 0\)
\( \Leftrightarrow - {a^2} - 2a + 3a + 6 = 0 \)\(\Leftrightarrow - a\left( {a + 2} \right) + 3\left( {a + 2} \right) = 0\) \( \Leftrightarrow \left( {a + 2} \right)\left( { - a + 3} \right) = 0\)\( \Leftrightarrow \left[ \begin{array}{l}a = - 2\\a = 3\end{array} \right.\)
Vậy có hai giá trị của $a$ thỏa mãn điều kiện đề bài $a = - 2;a = 3$ .
Tìm \(a\) và \(b\) để đa thức \(f\left( x \right) = {x^4} - 9{x^3} + 21{x^2} + ax + b\) chia hết cho đa thức \(g\left( x \right) = {x^2} - x - 2\)
Ta có

Phần dư của phép chia \(f\left( x \right)\) cho \(g\left( x \right)\) là \(R = \left( {a - 1} \right)x + b + 30\)
Để phép chia trên là phép chia hết thì \(R = 0\) với \(\forall x\) \( \Leftrightarrow \left( {a - 1} \right)x + b + 30 = 0\) với \(\forall x\)
\( \Leftrightarrow \left\{ \begin{array}{l}a - 1 = 0\\b + 30 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = - 30\end{array} \right.\) . Vậy \(a = 1;\,b = - 30\).
Biết đa thức ${x^4} + a{x^2} + b$ chia hết cho ${x^2}-x + 1$ . Khi đó, khẳng định nào sau đây là đúng.
Ta có
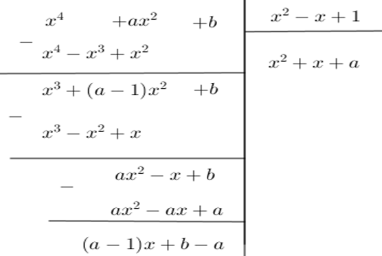
Phần dư của phép chia là \(R = \left( {a - 1} \right)x + b - a\) . Để phép chia trên là phép chia hết thì $R = 0,\,\forall x \Leftrightarrow \left( {a - 1} \right)x + b - a = 0,\,\forall x$ \( \Leftrightarrow \left\{ \begin{array}{l}a - 1 = 0\\b - a = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = 1\end{array} \right. \Leftrightarrow a = b\) .
Cho đa thức \(f(x) = {x^4} - 3{{\rm{x}}^3} + 3{{\rm{x}}^2} + {\rm{ax}} + b\) và đa thức \(g(x) = {x^2} - 3{\rm{x}} + 4\). Biết \(f\left( x \right)\) chia hết cho \(g\left( x \right)\) . Khi đó tích \(a.b\) bằng
Ta có
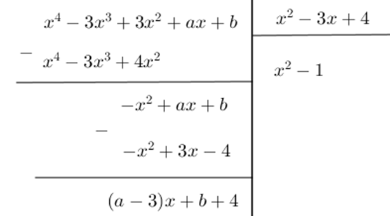
Phần dư của phép chia $f\left( x \right)$ cho \(g\left( x \right)\) là \(R = \left( {a - 3} \right)x + b + 4\) . Để phép chia trên là phép chia hết thì \(R = 0,\forall x \Leftrightarrow \left( {a - 3} \right)x + b + 4 = 0,\,\forall x \Leftrightarrow \left\{ \begin{array}{l}a - 3 = 0\\b + 4 = 0\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}a = 3\\b = - 4\end{array} \right. \Rightarrow ab = - 12\) .
Xác định a để \(\left( {6{x^3} - 7{x^2} - x + a} \right):\left( {2x + 1} \right)\) dư \(2\)
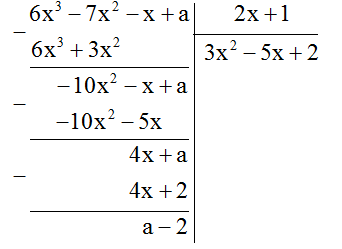
Để \(6{x^3} - 7{x^2} - x + a\) chia \(2x + 1\) dư \(2\) thì \(a - 2 = 2 \Leftrightarrow a = 4\).
Tìm các hằng số \(a\) và \(b\) sao cho \(\left( {{x^3} + ax + b} \right):\left( {x + 1} \right)\) dư 7 và \(\left( {{x^3} + ax + b} \right):\left( {x - 3} \right)\) dư \(\left( { - 5} \right)\)
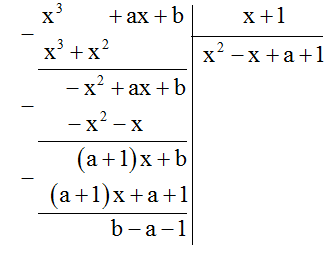
Để \({x^3} + ax + b\) chia cho \(x + 1\) dư \(7\) thì \(b - a - 1 = 7 \Leftrightarrow - a + b = 8\;(1)\)
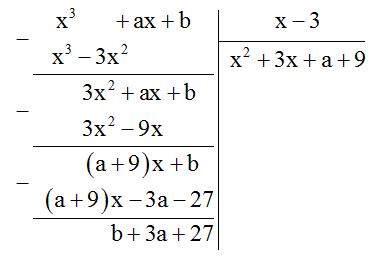
Để \({x^3} + ax + b\) chia cho \(x - 3\) dư \( - 5\) thì \(b + 3a + 27 = -5 \Leftrightarrow 3a + b = - 32\;(2)\)
Từ (1) và (2) ta có hệ \(\left\{ \begin{array}{l} - a + b = 8\\3a + b = - 32\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - 10\\b = - 2\end{array} \right.\)
Vậy \(a = - 10,b = - 2\).
Có bao nhiêu số nguyên \(x\) để giá trị của đa thức \(A = 2{x^3} - 3{x^2} + 2x + 2\) chia hết cho giá trị của đa thức \(B = {x^2} + 1\)
Ta có \(A:B\)
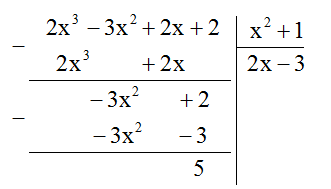
Để giá trị của đa thức \(A = 2{x^3} - 3{x^2} + 2x + 2\) chia hết cho giá trị của đa thức \(B = {x^2} + 1\) thì \(5\,\, \vdots \,\,\left( {{x^2} + 1} \right)\)
Hay \(\left( {{x^2} + 1} \right) \in U\left( 5 \right) = \left\{ { - 1;1; - 5;5} \right\}\)
+) \({x^2} + 1 = - 1 \Leftrightarrow {x^2} = - 2\left( {VL} \right)\)
+) \({x^2} + 1 = 1 \Leftrightarrow {x^2} = 0 \Leftrightarrow x = 0\left( {tm} \right)\)
+) \({x^2} + 1 = - 5 \Leftrightarrow {x^2} = - 6\left( {VL} \right)\)
+) \({x^2} + 1 = 5 \Leftrightarrow {x^2} = 4 \Leftrightarrow x = \pm 2\left( {tm} \right)\)
Vậy có 3 giá trị của \(x\) thỏa mãn đề bài là \(x = 0;x = - 2;x = 2.\)
Phần dư của phép chia đa thức \({\left( {{x^2} + 3x + 2} \right)^5} + {\left( {{x^2} - 4x - 4} \right)^5} - 1\) cho đa thức \(x + 1\) là
Ta có đa thức chia \(\left( {x + 1} \right)\) nên phần dư là một hằng số
Gọi thương là \(Q\left( x \right)\) và dư \(r\). Khi đó với mọi \(x\) ta có \({\left( {{x^2} + 3x + 2} \right)^5} + {\left( {{x^2} - 4x - 4} \right)^5} - 1 = Q\left( x \right)\left( {x + 1} \right) + r\) (1)
Thay \(x = - 1\) vào (1) ta được \({\left( {{{\left( { - 1} \right)}^2} + 3.\left( { - 1} \right) + 2} \right)^5} + {\left( {{{\left( { - 1} \right)}^2} - 4\left( { - 1} \right) - 4} \right)^5} - 1 = Q\left( x \right).\left( { - 1 + 1} \right) + r\)
\(r = {0^5} + {1^5} - 1 \Leftrightarrow r = 0\)
Vậy phần dư của phép chia là \(r = 0.\)
\(P = \dfrac{{2{n^3} - 3{n^2} + 3n - 1}}{{n - 1}}\). Tìm \(n \in Z\) để \(P \in Z\).
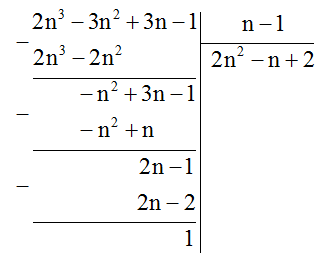
\(2{n^3} - 3{n^2} + 3n - 1 = \left( {2{n^2} - n + 2} \right)\left( {n - 1} \right) + 1\)
Để \(2{n^3} - 3{n^2} + 3n - 1\) chia hết cho \(n - 1\) thì \(1\) chia hết cho \(n - 1\).
\( \Rightarrow \left( {n - 1} \right) \in \left\{ {1, - 1} \right\}\)
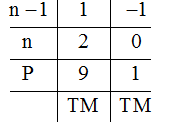
Vậy \(n \in \left\{ {0,2} \right\}\) để \(P \in Z\).

