Câu hỏi:
2 năm trước
Có bao nhiêu số nguyên \(x\) để giá trị của đa thức \(A = 2{x^3} - 3{x^2} + 2x + 2\) chia hết cho giá trị của đa thức \(B = {x^2} + 1\)
Trả lời bởi giáo viên
Đáp án đúng: a
Ta có \(A:B\)
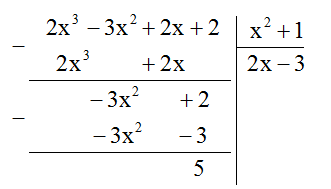
Để giá trị của đa thức \(A = 2{x^3} - 3{x^2} + 2x + 2\) chia hết cho giá trị của đa thức \(B = {x^2} + 1\) thì \(5\,\, \vdots \,\,\left( {{x^2} + 1} \right)\)
Hay \(\left( {{x^2} + 1} \right) \in U\left( 5 \right) = \left\{ { - 1;1; - 5;5} \right\}\)
+) \({x^2} + 1 = - 1 \Leftrightarrow {x^2} = - 2\left( {VL} \right)\)
+) \({x^2} + 1 = 1 \Leftrightarrow {x^2} = 0 \Leftrightarrow x = 0\left( {tm} \right)\)
+) \({x^2} + 1 = - 5 \Leftrightarrow {x^2} = - 6\left( {VL} \right)\)
+) \({x^2} + 1 = 5 \Leftrightarrow {x^2} = 4 \Leftrightarrow x = \pm 2\left( {tm} \right)\)
Vậy có 3 giá trị của \(x\) thỏa mãn đề bài là \(x = 0;x = - 2;x = 2.\)
Hướng dẫn giải:
- Đặt phép chia.
- Để thỏa mãn điều kiện của đề bài thì số dư cuối cùng phải chia hết cho số chia. Suy ra, số chia là ước của số dư cuối cùng.
- Lập bảng thử chọn để chọn ra giá trị của \(n\) thỏa mãn.
Câu hỏi khác
- Bài tập nhân đơn thức với đa thức, đa thức với đa thức toán 8 có lời giải
- Bài tập phân tích đa thức thành nhân tử bằng cách đặt nhân tử chung toán 8 có lời giải
- Bài tập những hằng đẳng thức đáng nhớ (tiếp) toán 8 có lời giải
- Bài tập phân tích đa thức thành nhân tử bằng cách dùng hằng đẳng thức toán 8 có lời giải
- Bài tập những hằng đẳng thức đáng nhớ toán 8 có lời giải
