Đề thi khảo sát chất lượng đầu năm - Đề số 5

$- {x^3}{\left( {xy} \right)^4}\dfrac{1}{3}{x^2}{y^3}{z^3} =  - \dfrac{1}{3}{x^5}.{x^4}.{y^4}.{y^3}.{z^3} =  - \dfrac{1}{3}{x^9}.{y^7}.{z^3}$

Theo kết quả câu trước ta có: $M\left( x \right) = 2{x^2} - 7x;N\left( x \right) = 11x - 10$.

Ta có:

$\begin{array}{l}M\left( x \right) = 0 \Leftrightarrow 2{x^2} - 7x = 0\\ \Leftrightarrow x\left( {2x - 7} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 0\\2x - 7 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \dfrac{7}{2}\end{array} \right.\end{array}$.

Và $N\left( x \right) = 0 \Leftrightarrow 11x - 10 = 0 \Leftrightarrow x = \dfrac{{10}}{{11}}$.

Vậy $M\left( x \right)$ có hai nghiệm và $N\left( x \right)$ có một nghiệm.

Ta có:

$\begin{array}{l} + )\,M\left( x \right) = P\left( x \right) + Q\left( x \right)\\ = {x^2} + 2x - 5 + {x^2} - 9x + 5 = 2{x^2} - 7x\end{array}$

$\begin{array}{l} + )\,N\left( x \right) = P\left( x \right) - Q\left( x \right)\\ = {x^2} + 2x - 5 - \left( {{x^2} - 9x + 5} \right)\\ = {x^2} + 2x - 5 - {x^2} + 9x - 5\\ = 11x - 10\end{array}$.

Vậy $M\left( x \right) = 2{x^2} - 7x;N\left( x \right) = 11x - 10$.

Ta có:

$\begin{array}{l} + )\,M\left( x \right) = P\left( x \right) + Q\left( x \right)\\ = {x^2} + 2x - 5 + {x^2} - 9x + 5 = 2{x^2} - 7x\end{array}$

$\begin{array}{l} + )\,N\left( x \right) = P\left( x \right) - Q\left( x \right)\\ = {x^2} + 2x - 5 - \left( {{x^2} - 9x + 5} \right)\\ = {x^2} + 2x - 5 - {x^2} + 9x - 5\\ = 11x - 10\end{array}$.

Vậy $M\left( x \right) = 2{x^2} - 7x;N\left( x \right) = 11x - 10$.

+) Xét $\Delta BEK$ vuông tại $K$ có: $EB > BK$ (bất đẳng thức tam giác).

Mà $\left\{ \begin{array}{l}BK = AK\\AK = AC\end{array} \right.\,\,\left( {cmt} \right) \Rightarrow EB > AC.$

+) Xét $\Delta ABE$ có:

$\left\{ \begin{array}{l}BD\, \bot \,AE\\EK\, \bot \,AB\\AC\, \bot \,BE\,\end{array} \right.\,\,\left( {gt} \right)$.

Suy ra: $BD,\,EK,\,AC$ là ba đường cao của $\Delta ABE$, 

Mà trong một tam giác ba đường cao đồng quy tại một điểm.

Vậy 3 đường thẳng $BD,\,EK,\,AC$ đồng quy.

Xét $\Delta ABC$ vuông tại $C$ ta có $\angle B + \angle BAC = {90^0} \Rightarrow \angle B = {90^0} - \angle BAC = {90^0} - {60^0} = {30^0}$.

Vì $AE$ là phân giác của $\angle BAC\,\,\left( {gt} \right)\, \Rightarrow \angle EBA\, = \dfrac{1}{2}\angle BAC = \dfrac{1}{2}{.60^0} = {30^0}$ (tính chất tia phân giác)

$\Rightarrow \angle EBA\,\, = \,\angle EAB\, = {30^0} \Rightarrow \Delta ABE$ cân tại $E$ (dấu hiệu nhận biết tam giác cân).

Mà $EK \bot AB\,\left( {gt} \right) \Rightarrow EK$ cũng là đường trung trực của $AB$ (tính chất tam giác cân)

$\Rightarrow AB = 2AK$ (tính chất đường trung trực)

Mà theo câu trước ta có: $AK = AC\,\, \Rightarrow AB = 2AC.$

Vì $AE$ là phân giác của $\angle CAK\,\left( {gt} \right) \Rightarrow \angle CAE = \angle BAE$ (tính chất tia phân giác).

Xét hai tam giác vuông $\Delta ACE$ và $\Delta AKE$ có:

+) $AE$ chung (gt)

+) $\angle CAE = \angle BAE\,\left( {cmt} \right)$

$\Rightarrow \Delta ACE = \Delta AKE$ (cạnh huyền – góc nhọn)

$\Rightarrow AC = AK$ (hai cạnh tương ứng)

Vì $\Delta ACE = \Delta AKE\,\left( {cmt} \right)\, \Rightarrow \,\,CE = \,EK$ (hai cạnh tương ứng) (1)

Vì $AC = AK\,\,\left( {cmt} \right)$ (2)

Từ (1) và (2) suy ra $AE$ là đường trung trực của $CK$ (dấu hiệu nhận biết đường trung trực của đoạn thẳng)

$\Rightarrow CK \bot \,\,AE$ (tính chất đường trung trực của đoạn thẳng).

Vì $AE$ là phân giác của $\angle CAK\,\left( {gt} \right) \Rightarrow \angle CAE = \angle BAE$ (tính chất tia phân giác).

Xét hai tam giác vuông $\Delta ACE$ và $\Delta AKE$ có:

+) $AE$ chung (gt)

+) $\angle CAE = \angle BAE\,\left( {cmt} \right)$

$\Rightarrow \Delta ACE = \Delta AKE$ (cạnh huyền – góc nhọn)

$\Rightarrow AC = AK$ (hai cạnh tương ứng)

Vì $\Delta ACE = \Delta AKE\,\left( {cmt} \right)\, \Rightarrow \,\,CE = \,EK$ (hai cạnh tương ứng) (1)

Vì $AC = AK\,\,\left( {cmt} \right)$ (2)

Từ (1) và (2) suy ra $AE$ là đường trung trực của $CK$ (dấu hiệu nhận biết đường trung trực của đoạn thẳng)

$\Rightarrow CK \bot \,\,AE$ (tính chất đường trung trực của đoạn thẳng).

Đơn thức cần điền vào dấu ba chấm là:

$- 3{x^3} - 3{x^3} = \left( { - 3 - 3} \right){x^3} =  - 6{x^3}$.

$\begin{array}{l}C + B = A \Rightarrow C = A - \,B = 3{x^2} - 7xy - \dfrac{3}{4} - \left( { - 0,75 + 2{x^2} + 7xy} \right)\\ = 3{x^2} - 7xy - \dfrac{3}{4} + 0,75 - 2{x^2} - 7xy = {x^2} - 14xy\end{array}$.

$P\left( x \right) + Q\left( x \right) =  - {x^3} + 2{x^2} + x - 1 + {x^3} - {x^2} - x + 2 = {x^2} + 1$

$P\left( x \right) + Q\left( x \right) = 0 \Leftrightarrow {x^2} + 1 = 0 \Leftrightarrow {x^2} =  - 1\,\,$ (vô nghiệm vì ${x^2} \ge 0$ với mọi $x$)

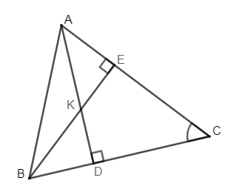
Xét ${\Delta}BEC$ vuông tại $E$, ta có: $\angle E = {90^0} \Rightarrow \angle C + \angle EBC = {90^0}$$\Rightarrow \angle EBC = {90^0} - \angle C$$= {90^0} - {50^0} = {40^0}$ nên kết luận của đáp án B đúng.

Xét ${\Delta}BKD$ vuông tại $D$, ta có: $\angle D = {90^0}$$\Rightarrow \angle KBD + \angle BKD = {90^0}$$\Rightarrow \angle BKD = {90^0} - \angle KBD = {90^0} - {40^0} = {50^0}$

Mà $\angle BKD + \angle BKA = {180^0} \Rightarrow \angle BKA = {180^0} - \angle BKD$$= {180^0} - {50^0} = {130^0}$  nên kết luận của đáp án A đúng.

Xét ${\Delta }ADC$ vuông tại $D$, ta có:

$\begin{array}{l}\angle D = {90^0} \Rightarrow \angle DAC + \angle C = {90^0}\\ \Rightarrow \angle DAC = {90^0} - \angle C = {90^0} - {50^0} = {40^0}\\ \Rightarrow \angle K{\rm{A}}C = \angle EBC\end{array}$.

Nên kết luận của đáp án D đúng.

Vậy kết luận của đáp án C sai.

Xét $\Delta ABC$ có: $\angle A + \angle B + \angle C = {180^0} \Rightarrow \angle A = {180^0} - \angle B - \angle C = {180^0} - {50^0} - {60^0} = {70^0}$ (định lý tổng ba góc trong tam giác).

Vì $\angle C < \angle B < \angle A\,\,\left( {{{50}^0} < {{60}^0} < {{70}^0}} \right) \Rightarrow AB < AC < BC$ (bất đẳng thức tam giác).

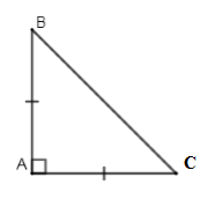
Vì $AB = AC\,\left( {gt} \right) \Rightarrow \Delta ABC$ cân tại $A$ (dấu hiệu nhận biết tam giác cân)

$\Rightarrow \angle B = \angle C$ (tính chất tam giác cân).

Ta có: $\angle A + \angle B + \angle C = {180^0}$ (định lý tổng ba góc của tam giác).

Mà $\left\{ \begin{array}{l}\angle B = \angle C\\\angle A = 2\angle B\\\angle A + \angle B + \angle C = {180^0}\end{array} \right. \\\Rightarrow 2\angle B + 2\angle C = {180^0} \\\Rightarrow \angle B + \angle C = {180^0}:2 = {90^0}\\ \Rightarrow \angle A = {180^0} - {90^0} = {90^0}$

$\Rightarrow \Delta ABC$ là tam giác vuông cân tại $A$ (dấu hiệu nhận biết tam giác vuông cân).

Ta có:

$\begin{array}{l}\,{\left( {3x - \dfrac{1}{2}} \right)^2} + \dfrac{{21}}{{25}} = 1\\\,\,{\left( {3x - \dfrac{1}{2}} \right)^2}\,\,= 1 - \dfrac{{21}}{{25}}\\\,\,\,{\left( {3x - \dfrac{1}{2}} \right)^2}\,\,\, = \dfrac{4}{{25}}\\\,\,\,{\left( {3x - \dfrac{1}{2}} \right)^2}\,\,\, = \,{\left( { \pm \dfrac{2}{5}} \right)^2}\end{array}$

TH1:

$\begin{array}{l}3x - \dfrac{1}{2} = \dfrac{2}{5}\\3x\,\,\, = \dfrac{2}{5} + \dfrac{1}{2} = \dfrac{9}{{10}}\\\,\,\,x\,\,\, = \dfrac{9}{{10}}:3\\\,\,\,x\,\,\, = \dfrac{3}{{10}}\end{array}$

TH2:

$\begin{array}{l}3x - \dfrac{1}{2} =  - \dfrac{2}{5}\\3x\,\,\, =  - \dfrac{2}{5} + \dfrac{1}{2} = \dfrac{1}{{10}}\\\,\,\,x\,\,\, = \dfrac{1}{{10}}:3\\\,\,\,x\,\,\, = \dfrac{1}{{30}}\end{array}$

Vậy $x = \dfrac{3}{{10}}$ hoặc $x = \dfrac{1}{{30}}$.

$\begin{array}{l}\,25\dfrac{3}{{19}}:\left( {\dfrac{{ - 5}}{4}} \right) - 35\dfrac{3}{{19}}:\left( {\dfrac{{ - 5}}{4}} \right)\\ = \left( {25\dfrac{3}{{19}} - 35\dfrac{3}{{19}}} \right):\left( {\dfrac{{ - 5}}{4}} \right)\\ = \left( {25 + \dfrac{3}{{19}} - 35 - \dfrac{3}{{19}}} \right):\left( {\dfrac{{ - 5}}{4}} \right)\\ =  - 10:\dfrac{{ - 5}}{4}\\ = \dfrac{{ - 40}}{{ - 5}}\\ = 8\end{array}$.

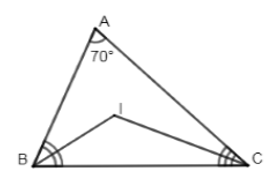
Vì $BI$ và $CI$ là tia phân giác của $\angle ABC$ và $\angle ACB\,\,\left( {gt} \right)$

$\Rightarrow \left\{ \begin{array}{l}\angle IBC = \dfrac{1}{2}\angle ABC\\\angle ICB = \dfrac{1}{2}\angle ACB\end{array} \right.$ (tính chất tia phân giác)

$\Rightarrow \angle IBC + \angle ICB = \dfrac{1}{2}\left( {\angle ABC + \angle ACB} \right) = \dfrac{1}{2}\left( {{{180}^0} - \angle A} \right) = \dfrac{1}{2}\left( {{{180}^0} - {{70}^0}} \right) = \dfrac{1}{2}{.110^0} = {55^0}$

Xét $\Delta BIC$ có: $\angle BIC + \angle IBC + \angle ICB = {180^0}$ (tổng ba góc trong tam giác)

$\Rightarrow \angle BIC = {180^0} - \left( {\angle IBC + \angle ICB} \right) = {180^0} - {55^0} = {125^0}$.

Ta có: $\left( {3x - 2} \right)\left( {3x + 2} \right) = {\left( {3x} \right)^2} - {2^2} = 9{x^2} - 4$.

Ta có:

$\begin{array}{l}\,\,\,2{x^2} + 7x - 9 = 0\\ \Leftrightarrow 2{x^2} + 9x - 2x - 9 = 0\\ \Leftrightarrow x\left( {2x + 9} \right) - \left( {2x + 9} \right) = 0\\ \Leftrightarrow \left( {2x + 9} \right)\left( {x - 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}2x + 9 = 0\\x - 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{{ - 9}}{2}\\x = 1\end{array} \right.\end{array}$.

Vậy có hai nghiệm là $x =  - \dfrac{9}{2};x = 1.$

Ta có:

$\begin{array}{l}7{x^3} + 3{x^4} - x + 5{x^2} - 6{x^3} - 2{x^4} + 2020 + {x^3}\\ = 3{x^4} - 2{x^4} + 7{x^3} - 6{x^3} + {x^3} - x + 2020\\ = {x^4} + 2{x^3} - x + 2020\end{array}$.

 Hệ số cao nhất là: $1$, hệ số tự do là $2020$.