Cho 2 đa thức \(P\left( x \right) = {x^2} + 2x - 5\) và \(Q\left( x \right) = {x^2} - 9x + 5\).
Tính \(M\left( x \right) = P\left( x \right) + Q\left( x \right);\,N\left( x \right) = P\left( x \right) - Q\left( x \right)\).
Ta có:
\(\begin{array}{l} + )\,M\left( x \right) = P\left( x \right) + Q\left( x \right)\\ = {x^2} + 2x - 5 + {x^2} - 9x + 5 = 2{x^2} - 7x\end{array}\)
\(\begin{array}{l} + )\,N\left( x \right) = P\left( x \right) - Q\left( x \right)\\ = {x^2} + 2x - 5 - \left( {{x^2} - 9x + 5} \right)\\ = {x^2} + 2x - 5 - {x^2} + 9x - 5\\ = 11x - 10\end{array}\).
Vậy \(M\left( x \right) = 2{x^2} - 7x;N\left( x \right) = 11x - 10\).
Cho 2 đa thức \(P\left( x \right) = {x^2} + 2x - 5\) và \(Q\left( x \right) = {x^2} - 9x + 5\).
Chọn câu đúng về ghiệm các đa thức \(M\left( x \right);\,N\left( x \right)\).
Theo kết quả câu trước ta có: \(M\left( x \right) = 2{x^2} - 7x;N\left( x \right) = 11x - 10\).
Ta có:
\(\begin{array}{l}M\left( x \right) = 0 \Leftrightarrow 2{x^2} - 7x = 0\\ \Leftrightarrow x\left( {2x - 7} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 0\\2x - 7 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \dfrac{7}{2}\end{array} \right.\end{array}\).
Và \(N\left( x \right) = 0 \Leftrightarrow 11x - 10 = 0 \Leftrightarrow x = \dfrac{{10}}{{11}}\).
Vậy \(M\left( x \right)\) có hai nghiệm và \(N\left( x \right)\) có một nghiệm.
Tính giá trị của đa thức \(f\left( x \right) = {x^6} - 2019{x^5} + 2019{x^4} - 2019{x^3} + 2019{x^2} - 2019x + 1\) tại \(x = 2018\).
\(\begin{array}{l}\,f\left( x \right) = {x^6} - 2019{x^5} + 2019{x^4} - 2019{x^3} + 2019{x^2} - 2019x + 1\\ = {x^6} - \left( {2018 + 1} \right)\left( {{x^5} - {x^4} + {x^3} - {x^2} + x} \right) + 1\\ = {x^6} - 2018{x^5} - {x^5} + 2018{x^4} + {x^4} - 2018{x^3} - {x^3} + 2018{x^2} + {x^2} - 2018x - x + 1\end{array}\).
Thay \(x = 2018\) vào đa thức \(f\left( x \right)\) ta được:
\(f\left( {2018} \right) = {2018^6} - {2018^6} - {2018^5} + {2018^5} + {2018^4} - {2018^4} - {2018^3}\)\( + {2018^3} + {2018^2} - {2018^2} - 2018 + 1\)
\( = - 2018 + 1 = - 2017\).
Cho \(\Delta ABC\) vuông tại \(C\) có: \(\widehat A = {60^0}\). Tia phân giác \(\widehat {BAC}\) cắt \(BC\) ở \(E\). Kẻ \(EK\) vuông góc với \(AB\) ở \(K\). Kẻ \(BD\) vuông góc với \(AE\) ở \(D\).
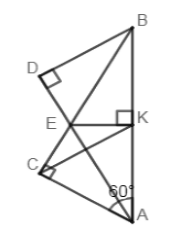
Chọn câu đúng nhất.
Vì \(AE\) là phân giác của \(\angle CAK\,\left( {gt} \right) \Rightarrow \angle CAE = \angle BAE\) (tính chất tia phân giác).
Xét hai tam giác vuông \(\Delta ACE\) và \(\Delta AKE\) có:
+) \(AE\) chung (gt)
+) \(\angle CAE = \angle BAE\,\left( {cmt} \right)\)
\( \Rightarrow \Delta ACE = \Delta AKE\) (cạnh huyền – góc nhọn)
\( \Rightarrow AC = AK\) (hai cạnh tương ứng)
Vì \(\Delta ACE = \Delta AKE\,\left( {cmt} \right)\, \Rightarrow \,\,CE = \,EK\) (hai cạnh tương ứng) (1)
Vì \(AC = AK\,\,\left( {cmt} \right)\) (2)
Từ (1) và (2) suy ra \(AE\) là đường trung trực của \(CK\) (dấu hiệu nhận biết đường trung trực của đoạn thẳng)
\( \Rightarrow CK \bot \,\,AE\) (tính chất đường trung trực của đoạn thẳng).
Cho \(\Delta ABC\) vuông tại \(C\) có: \(\widehat A = {60^0}\). Tia phân giác \(\widehat {BAC}\) cắt \(BC\) ở \(E\). Kẻ \(EK\) vuông góc với \(AB\) ở \(K\). Kẻ \(BD\) vuông góc với \(AE\) ở \(D\).

Mối quan hệ đúng là:
Xét \(\Delta ABC\) vuông tại \(C\) ta có \(\angle B + \angle BAC = {90^0} \Rightarrow \angle B = {90^0} - \angle BAC = {90^0} - {60^0} = {30^0}\).
Vì \(AE\) là phân giác của \(\angle BAC\,\,\left( {gt} \right)\, \Rightarrow \angle EBA\, = \dfrac{1}{2}\angle BAC = \dfrac{1}{2}{.60^0} = {30^0}\) (tính chất tia phân giác)
\( \Rightarrow \angle EBA\,\, = \,\angle EAB\, = {30^0} \Rightarrow \Delta ABE\) cân tại \(E\) (dấu hiệu nhận biết tam giác cân).
Mà \(EK \bot AB\,\left( {gt} \right) \Rightarrow EK\) cũng là đường trung trực của \(AB\) (tính chất tam giác cân)
\( \Rightarrow AB = 2AK\) (tính chất đường trung trực)
Mà theo câu trước ta có: \(AK = AC\,\, \Rightarrow AB = 2AC.\)
Cho \(\Delta ABC\) vuông tại \(C\) có: \(\widehat A = {60^0}\). Tia phân giác \(\widehat {BAC}\) cắt \(BC\) ở \(E\). Kẻ \(EK\) vuông góc với \(AB\) ở \(K\). Kẻ \(BD\) vuông góc với \(AE\) ở \(D\).

Chọn câu đúng nhất.
+) Xét \(\Delta BEK\) vuông tại \(K\) có: \(EB > BK\) (bất đẳng thức tam giác).
Mà \(\left\{ \begin{array}{l}BK = AK\\AK = AC\end{array} \right.\,\,\left( {cmt} \right) \Rightarrow EB > AC.\)
+) Xét \(\Delta ABE\) có:
\(\left\{ \begin{array}{l}BD\, \bot \,AE\\EK\, \bot \,AB\\AC\, \bot \,BE\,\end{array} \right.\,\,\left( {gt} \right)\).
Suy ra: \(BD,\,EK,\,AC\) là ba đường cao của \(\Delta ABE\),
Mà trong một tam giác ba đường cao đồng quy tại một điểm.
Vậy 3 đường thẳng \(BD,\,EK,\,AC\) đồng quy.
Cho đa thức \(f\left( x \right) = a{x^2} + bx + c\). Tính giá trị của \(f\left( { - 1} \right)\) biết \(a + c = b + 2018\).
Ta có:
\(f\left( { - 1} \right) = a.{\left( { - 1} \right)^2} + b.\left( { - 1} \right) + c = \,a - b + c = \,\left( {a + c} \right) - b\).
Mà \(a + c = b + 2018 \Rightarrow f\left( { - 1} \right) = b + 2018 - b = 2018\). Vậy \(f\left( { - 1} \right) = 2018\).
Cho đa thức \(F\left( x \right) = a{x^2} + bx + c\) với các hệ số \(a,\,b,\,c\) thỏa mãn \(11a - b + 5c = 0\).
Chọn câu đúng.
Ta có:
\(\begin{array}{l}F\left( 1 \right) = a + b + c \Rightarrow 3F\left( 1 \right) = 3a + 3b + 3c\\F\left( { - 2} \right) = 4a - 2b + c \Rightarrow 2F\left( { - 2} \right) = 8a - 4b + 2c\end{array}\).
Xét:
\(\begin{array}{l}3F\left( 1 \right) = 3a + 3b + 3c = 11a - 8a + 4b - b + 5c - 2c\\ = \left( {11a - b + 5c} \right) - \left( {8a - 4b + 2c} \right) = 0 - 2F\left( { - 2} \right) = - 2F\left( { - 2} \right)\\ \Rightarrow 3F\left( 1 \right) = - 2F\left( { - 2} \right)\end{array}\).
Suy ra: \(F\left( 1 \right)\) và \(F\left( { - 2} \right)\) không thể cùng dấu hay \(F\left( 1 \right);F\left( { - 2} \right)\) trái dấu.

