Cho \(\Delta ABC\) vuông tại \(C\) có: \(\widehat A = {60^0}\). Tia phân giác \(\widehat {BAC}\) cắt \(BC\) ở \(E\). Kẻ \(EK\) vuông góc với \(AB\) ở \(K\). Kẻ \(BD\) vuông góc với \(AE\) ở \(D\).
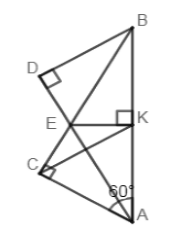
Mối quan hệ đúng là:
Trả lời bởi giáo viên
Xét \(\Delta ABC\) vuông tại \(C\) ta có \(\angle B + \angle BAC = {90^0} \Rightarrow \angle B = {90^0} - \angle BAC = {90^0} - {60^0} = {30^0}\).
Vì \(AE\) là phân giác của \(\angle BAC\,\,\left( {gt} \right)\, \Rightarrow \angle EBA\, = \dfrac{1}{2}\angle BAC = \dfrac{1}{2}{.60^0} = {30^0}\) (tính chất tia phân giác)
\( \Rightarrow \angle EBA\,\, = \,\angle EAB\, = {30^0} \Rightarrow \Delta ABE\) cân tại \(E\) (dấu hiệu nhận biết tam giác cân).
Mà \(EK \bot AB\,\left( {gt} \right) \Rightarrow EK\) cũng là đường trung trực của \(AB\) (tính chất tam giác cân)
\( \Rightarrow AB = 2AK\) (tính chất đường trung trực)
Mà theo câu trước ta có: \(AK = AC\,\, \Rightarrow AB = 2AC.\)
Hướng dẫn giải:
Sử dụng tính chất đường phân giác và tính chất đường trung trực của tam giác.

