Cho \(\Delta ABC\) vuông tại \(C\) có: \(\widehat A = {60^0}\). Tia phân giác \(\widehat {BAC}\) cắt \(BC\) ở \(E\). Kẻ \(EK\) vuông góc với \(AB\) ở \(K\). Kẻ \(BD\) vuông góc với \(AE\) ở \(D\).
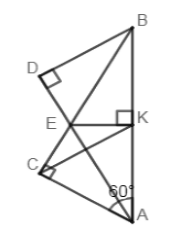
Chọn câu đúng nhất.
Trả lời bởi giáo viên
+) Xét \(\Delta BEK\) vuông tại \(K\) có: \(EB > BK\) (bất đẳng thức tam giác).
Mà \(\left\{ \begin{array}{l}BK = AK\\AK = AC\end{array} \right.\,\,\left( {cmt} \right) \Rightarrow EB > AC.\)
+) Xét \(\Delta ABE\) có:
\(\left\{ \begin{array}{l}BD\, \bot \,AE\\EK\, \bot \,AB\\AC\, \bot \,BE\,\end{array} \right.\,\,\left( {gt} \right)\).
Suy ra: \(BD,\,EK,\,AC\) là ba đường cao của \(\Delta ABE\),
Mà trong một tam giác ba đường cao đồng quy tại một điểm.
Vậy 3 đường thẳng \(BD,\,EK,\,AC\) đồng quy.
Hướng dẫn giải:
Sử dụng bất đẳng thức tam giác và tính chất ba đường cao của tam giác.

