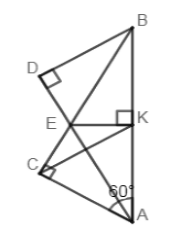
Cho \(\Delta ABC\) vuông tại \(C\) có: \(\widehat A = {60^0}\). Tia phân giác \(\widehat {BAC}\) cắt \(BC\) ở \(E\). Kẻ \(EK\) vuông góc với \(AB\) ở \(K\). Kẻ \(BD\) vuông góc với \(AE\) ở \(D\).
Chọn câu đúng nhất.
Trả lời bởi giáo viên
Vì \(AE\) là phân giác của \(\angle CAK\,\left( {gt} \right) \Rightarrow \angle CAE = \angle BAE\) (tính chất tia phân giác).
Xét hai tam giác vuông \(\Delta ACE\) và \(\Delta AKE\) có:
+) \(AE\) chung (gt)
+) \(\angle CAE = \angle BAE\,\left( {cmt} \right)\)
\( \Rightarrow \Delta ACE = \Delta AKE\) (cạnh huyền – góc nhọn)
\( \Rightarrow AC = AK\) (hai cạnh tương ứng)
Vì \(\Delta ACE = \Delta AKE\,\left( {cmt} \right)\, \Rightarrow \,\,CE = \,EK\) (hai cạnh tương ứng) (1)
Vì \(AC = AK\,\,\left( {cmt} \right)\) (2)
Từ (1) và (2) suy ra \(AE\) là đường trung trực của \(CK\) (dấu hiệu nhận biết đường trung trực của đoạn thẳng)
\( \Rightarrow CK \bot \,\,AE\) (tính chất đường trung trực của đoạn thẳng).
Hướng dẫn giải:
Áp dụng dấu hiệu nhận biết đường trung trực của đoạn thẳng, tính chất tam giác cân, tính chất tia phân giác, hai tam giác bằng nhau.

