Cho hình bên biết \(AB = 8cm,AC = 16cm\), \(\widehat {ABD} = \widehat {BCA}\). Độ dài đoạn \(AD\) là:
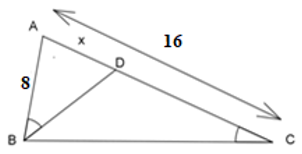
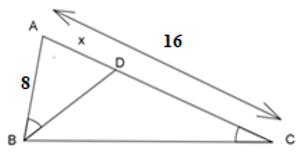
Xét \(\Delta ABD\) và \(\Delta ACB\) có:
\(\widehat A\;chung\)
\(\widehat {ABD} = \widehat {BCA}\;(gt)\)
\( \Rightarrow \Delta ABD\backsim\Delta ACB\;(g - g)\)
\( \Rightarrow \dfrac{{AB}}{{AC}} = \dfrac{{AD}}{{AB}}\)\( \Leftrightarrow \dfrac{x}{8} = \dfrac{8}{{16}} \Leftrightarrow x = \dfrac{{8.8}}{{16}} = 4cm\).
Cho hai tam giác \(ABC\) và \(DEF\) có: \(\widehat A = {40^0},\widehat B = {80^0}\), \(\widehat E = {40^0},\widehat D = {60^0}\). Chọn câu đúng.
Tam giác \(ABC\) có: \(\widehat A + \widehat B + \widehat C = {180^0}\)\( \Rightarrow \widehat C = {180^0} - {40^0} - {80^0} = {60^0}\)
Tam giác \(DEF\) có: \(\widehat D + \widehat E + \widehat F = {180^0}\) \( \Rightarrow \widehat F = {180^0} - \widehat D - \widehat E\) \( = {180^0} - {40^0} - {60^0} = {80^0}\).
Xét \(\Delta ABC\) và \(\Delta EFD\) có:
\(\widehat A = \widehat E = {40^0}\)
\(\widehat C = \widehat D = {60^0}\)
\( \Rightarrow \Delta ABC\backsim\Delta EFD\,(g - g)\) hay \(\Delta CBA \backsim \Delta DFE\).
Cho hai tam giác \(ABC\) và \(DEF\) có: \(\widehat A = {40^0},\widehat B = {80^0}\), \(\widehat E = {40^0},\widehat D = {60^0}\). Chọn câu đúng.
Tam giác \(ABC\) có: \(\widehat A + \widehat B + \widehat C = {180^0}\)\( \Rightarrow \widehat C = {180^0} - {40^0} - {80^0} = {60^0}\)
Tam giác \(DEF\) có: \(\widehat D + \widehat E + \widehat F = {180^0}\) \( \Rightarrow \widehat F = {180^0} - \widehat D - \widehat E\) \( = {180^0} - {40^0} - {60^0} = {80^0}\).
Xét \(\Delta ABC\) và \(\Delta EFD\) có:
\(\widehat A = \widehat E = {40^0}\)
\(\widehat C = \widehat D = {60^0}\)
\( \Rightarrow \Delta ABC\backsim\Delta EFD\,(g - g)\) hay \(\Delta CBA \backsim \Delta DFE\).
Cho tam giác \(ABC\) vuông tại \(A\) có: \(AB = 5,AC = 12\). Trên cạnh \(BC\) lấy điểm \(M\) sao cho \(BM = \dfrac{5}{{13}}BC\). Qua \(M\) kẻ đường thẳng vuông góc với \(AC\) tại \(N\). Độ dài \(MN\) là:
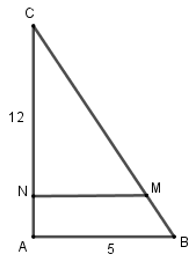
Tam giác \(ABC\) vuông tại \(A\), theo định lí Pi-ta-go ta có:
\(B{C^2} = A{B^2} + A{C^2}\) \( \Rightarrow B{C^2} = {5^2} + {12^2} = 169\) \( \Rightarrow BC = 13\).
\(BM = \dfrac{5}{{13}}BC = \dfrac{5}{{13}}.13 = 5\) \( \Rightarrow CM = 13 - 5 = 8\).
Xét \(\Delta CMN\) và \(\Delta CBA\) có:
\(\widehat N = \widehat A = {90^0}\) (gt)
\(\widehat C\) chung
\( \Rightarrow \Delta CMN \backsim \Delta CBA\left( {g - g} \right)\)\( \Rightarrow \dfrac{{MN}}{{AB}} = \dfrac{{CM}}{{CB}}\) (cạnh tương ứng)
\( \Rightarrow MN = \dfrac{{AB.CM}}{{CB}} = \dfrac{{5.8}}{{13}} = \dfrac{{40}}{{13}}\).
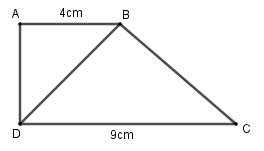
Cho hình thang vuông \(ABCD\left( {\widehat A = \widehat D = {{90}^0}} \right)\) có \(BC \bot BD\), \(AB = 4cm,CD = 9cm\). Độ dài \(BD\) là:
Xét tam giác \(ABD\) và \(BDC\) có:
\(\widehat {BAD} = \widehat {DBC} = {90^0}\)
\(\widehat {ABD} = \widehat {BDC}\) (so le trong)
\( \Rightarrow \Delta ABD \backsim \Delta BDC\left( {g - g} \right)\) \( \Rightarrow \dfrac{{AB}}{{BD}} = \dfrac{{BD}}{{DC}}\) (cạnh t/ư)
\( \Rightarrow B{D^2} = AB.CD = 4.9 = 36\) \( \Rightarrow BD = 6\).
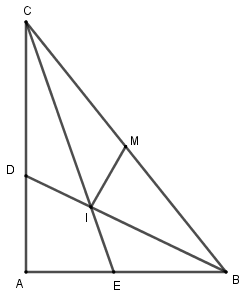
Tam giác đồng dạng với \(\Delta BIM\) là:
Theo câu a, \(DC = 5cm = CM\).
Xét \(\Delta CDI\) và \(\Delta CMI\) có:
\(\begin{array}{l}DC = MC\left( {cmt} \right)\\\widehat {DCI} = \widehat {MCI}\left( {phân\,giác\,CI} \right)\\chung\,CI\end{array}\)
\( \Rightarrow \Delta CDI = \Delta CMI\left( {c.g.c} \right)\) \( \Rightarrow \widehat {CDI} = \widehat {CMI}\) (góc t/ư)
\( \Rightarrow \widehat {ADB} = \widehat {BMI}\) (do \(\widehat {ADI} + \widehat {CDI} = {180^0} = \widehat {BMI} + \widehat {CMI}\))
Xét \(\Delta BIM\) và \(\Delta BAD\) có:
\(\widehat {MBI} = \widehat {ABD}\) (\(BD\) là phân giác góc \(\widehat B\))
\(\widehat {ADB} = \widehat {BMI}\left( {cmt} \right)\)
\( \Rightarrow \Delta BIM \backsim \Delta BAD\left( {g - g} \right)\).
Chọn khẳng định đúng.
Tam giác \(ABC\) vuông tại \(A\), theo định lý Pi – ta – go ta có:
\(B{C^2} = A{B^2} + A{C^2}\) \( = {6^2} + {8^2} = 100\) \( \Rightarrow BC = 10cm\).
Ta có: \(BD\) là phân giác góc \(B\) nên \(\dfrac{{DC}}{{DA}} = \dfrac{{BC}}{{BA}}\) hay \(\dfrac{{DC}}{{BC}} = \dfrac{{DA}}{{BA}} = \dfrac{{DC + DA}}{{BC + BA}}\) \( = \dfrac{8}{{10 + 6}} = \dfrac{1}{2}\)
\( \Rightarrow DC = \dfrac{1}{2}BC = \dfrac{1}{2}.10 = 5cm\).
Chọn khẳng định đúng.

Tam giác \(ABC\) vuông tại \(A\), theo định lý Pi – ta – go ta có:
\(B{C^2} = A{B^2} + A{C^2}\) \( = {6^2} + {8^2} = 100\) \( \Rightarrow BC = 10cm\).
Ta có: \(BD\) là phân giác góc \(B\) nên \(\dfrac{{DC}}{{DA}} = \dfrac{{BC}}{{BA}}\) hay \(\dfrac{{DC}}{{BC}} = \dfrac{{DA}}{{BA}} = \dfrac{{DC + DA}}{{BC + BA}}\) \( = \dfrac{8}{{10 + 6}} = \dfrac{1}{2}\)
\( \Rightarrow DC = \dfrac{1}{2}BC = \dfrac{1}{2}.10 = 5cm\).
Chọn khẳng định sai.
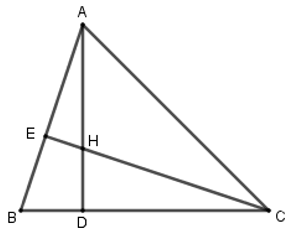
Theo câu a, \(\Delta ADB \backsim \Delta CDH\)\( \Rightarrow \dfrac{{BD}}{{DH}} = \dfrac{{AB}}{{CH}}\) (cạnh t/ư) nên D đúng.
Xét \(\Delta AHE\) và \(\Delta CHD\) có:
\(\widehat {AHE} = \widehat {CHD}\) (đối đỉnh)
\(\widehat {EAH} = \widehat {DCH}\left( {cmt} \right)\)
Suy ra \(\Delta AHE \backsim \Delta CHD\left( {g - g} \right)\)\( \Rightarrow \dfrac{{HA}}{{HC}} = \dfrac{{HE}}{{HD}}\) (cạnh t/ư)\( \Rightarrow \dfrac{{HA}}{{HE}} = \dfrac{{HC}}{{HD}}\).
Xét \(\Delta HAC\) và \(\Delta HED\) có:
\(\widehat {AHC} = \widehat {EHD}\) (đối đỉnh)
\(\dfrac{{HA}}{{HE}} = \dfrac{{HC}}{{HD}}\left( {cmt} \right)\)
Suy ra \(\Delta HAC \backsim \Delta HED\)(c-g-c)
\( \Rightarrow \widehat {HCA} = \widehat {HDE}\) (góc t/ư) hay C sai.
Chọn câu trả lời đúng nhất.
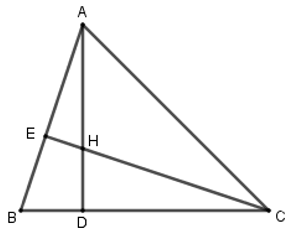
Xét tam giác \(ABD\) và \(CBE\) có:
\(\widehat E = \widehat D = {90^0}\)
Chung \(\widehat B\)
\( \Rightarrow \Delta ABD\backsim\Delta CBE\left( {g - g} \right)\).
\( \Rightarrow \widehat {BAD} = \widehat {BCE} = \widehat {DCH}\) (góc t/ư)
Xét \(\Delta ADB\) và \(\Delta CDH\) có:
\(\begin{array}{l}\widehat {ADB} = \widehat {CDH} = {90^0}\\\widehat {BAD} = \widehat {DCH}\left( {cmt} \right)\end{array}\)
\( \Rightarrow \Delta ADB \backsim \Delta CDH\left( {g - g} \right)\)
Vậy A, B đều đúng.
Chọn câu trả lời đúng nhất.

Xét tam giác \(ABD\) và \(CBE\) có:
\(\widehat E = \widehat D = {90^0}\)
Chung \(\widehat B\)
\( \Rightarrow \Delta ABD\backsim\Delta CBE\left( {g - g} \right)\).
\( \Rightarrow \widehat {BAD} = \widehat {BCE} = \widehat {DCH}\) (góc t/ư)
Xét \(\Delta ADB\) và \(\Delta CDH\) có:
\(\begin{array}{l}\widehat {ADB} = \widehat {CDH} = {90^0}\\\widehat {BAD} = \widehat {DCH}\left( {cmt} \right)\end{array}\)
\( \Rightarrow \Delta ADB \backsim \Delta CDH\left( {g - g} \right)\)
Vậy A, B đều đúng.
Cho hình bình hành \(ABCD\) có \(I\) là giao điểm của \(AC\) và \(BD\). \(E\) là một điểm bất kì thuộc \(BC\), qua \(E\) kẻ đường thẳng song song với \(AB\) và cắt \(BD,AC,AD\) lại \(G,H,F\). Chọn kết luận sai?
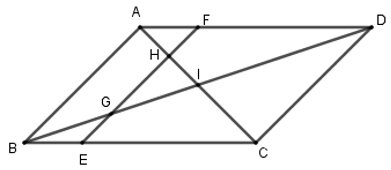
Có \(ABCD\) là hình bình hành nên:
\(AD{\rm{//}}BC, AB{\rm{//}}\,DC\)
Xét \(\Delta BGE\) và \(\Delta DGF\) có:
\(\widehat {BGE} = \widehat {DGF}\) (đối đỉnh)
\(\widehat {EBG} = \widehat {FDG}\) (so le trong)
\( \Rightarrow \Delta BGE \backsim \Delta DGF\) (g-g) nên C đúng.
Xét \(\Delta AHF\) và \(\Delta CHE\) có:
\(\widehat {AHF} = \widehat {CHE}\) (đối đỉnh)
\(\widehat {HAF} = \widehat {HCE}\) (so le trong)
\( \Rightarrow \Delta AHF \backsim \Delta CHE\left( {g - g} \right)\) nên D đúng.
Lại có \(GH//AB\) \( \Rightarrow \widehat {IHG} = \widehat {IAB}\) (đồng vị)
Xét \(\Delta GHI\) và \(\Delta BAI\) có:
Chung \(I\)
\(\widehat {IHG} = \widehat {IAB}\) (cmt)
\( \Rightarrow \Delta GHI \backsim \Delta BAI\left( {g - g} \right)\)
Suy ra B đúng.
Chỉ có A sai.
Tam giác \(ABC\) có: \(\widehat A = 2\widehat B\), \(AC = 16\,{\rm{cm}}\), \(BC = 20\,{\rm{cm}}\). Tính độ dài cạnh \(AB\).
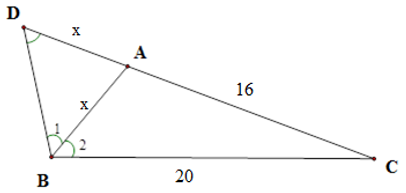
Trên tia đối của tia \(AC\) lấy điểm \(D\) sao cho \(AD = AB = x\).
Tam giác \(ABD\) cân tại \(A\) nên \(\widehat {BAC} = \widehat {{B_1}} + \widehat D = 2\widehat D\).
Ta lại có: \(\widehat {BAC} = 2\widehat {{B_2}}\) nên \(\widehat D = \widehat {{B_2}}\).
Xét \(\Delta CBA\) và \(\Delta CDB\) có: \(\widehat C\) chung và \(\widehat D = \widehat {{B_2}}\)
Nên \(\Delta CBA\backsim\Delta CDB\,\left( {g - g} \right)\) nên \(\dfrac{{CB}}{{CD}} = \dfrac{{AC}}{{BC}}\),
tức là \(\dfrac{{20}}{{16 + x}} = \dfrac{{16}}{{20}}\)\( \Leftrightarrow 16 + x = \dfrac{{20.20}}{{16}} = 25\) \( \Rightarrow x = 25 - 16 = 9\left( {cm} \right)\).
Vậy \(AB = 9cm\).
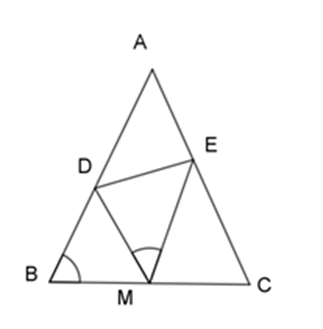
Chọn kết luận đúng.
Đặt \(\widehat B = \widehat C = x\), \(\widehat {BDM} = \widehat {EDM} = y,\)\(\widehat {CEM} = \widehat {DEM} = z\)
Tứ giác \(BDCE\) có: \(\widehat B + \widehat C + \widehat {BDE} + \widehat {CED} = {360^0}\)
\( \Rightarrow 2x + 2y + 2z = {360^0}\) \( \Leftrightarrow x + y + z = {180^0}\)
Hay \(\widehat B + \widehat {BDM} + \widehat {CEM} = {180^0}\)
Mà \(\widehat B + \widehat {BDM} + \widehat {BMD} = {180^0}\)(tổng ba góc trong tam giác)
Nên \(\widehat {CEM} = \widehat {BMD}\).
Xét \(\Delta BDM\) và \(\Delta CME\) có:
\(\begin{array}{l}\widehat B = \widehat C\left( {gt} \right)\\\widehat {BMD} = \widehat {CEM}\left( {cmt} \right)\end{array}\)
\( \Rightarrow \Delta BDM \backsim \Delta CME\left( {g - g} \right)\).
Chọn khẳng định đúng.
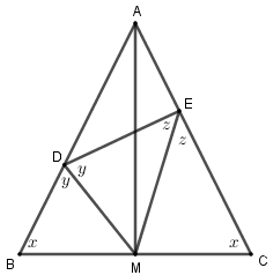
Tam giác \(ABC\) có: \(M\) là trung điểm của \(BC\) nên \(AM\) vừa là đường trung tuyến vừa là đường phân giác trong góc \(A\).
Lại có: \(DM\) là phân giác của góc \(\widehat {BDE}\) nên \(DM\) là phân giác ngoài góc \(D\) của tam giác \(ADE\).
Tam giác \(ADE\) có phân giác trong \(AM\) cắt phân giác ngoài \(DM\) tại \(M\) nên \(EM\) là đường phân giác ngoài góc \(E\) hay \(EM\) là phân giác của góc \(\widehat {DEC}\).
Vậy \(\widehat {DEM} = \widehat {CEM}\).
Chọn khẳng định đúng.

Tam giác \(ABC\) có: \(M\) là trung điểm của \(BC\) nên \(AM\) vừa là đường trung tuyến vừa là đường phân giác trong góc \(A\).
Lại có: \(DM\) là phân giác của góc \(\widehat {BDE}\) nên \(DM\) là phân giác ngoài góc \(D\) của tam giác \(ADE\).
Tam giác \(ADE\) có phân giác trong \(AM\) cắt phân giác ngoài \(DM\) tại \(M\) nên \(EM\) là đường phân giác ngoài góc \(E\) hay \(EM\) là phân giác của góc \(\widehat {DEC}\).
Vậy \(\widehat {DEM} = \widehat {CEM}\).
Tam giác \(MBC\) đồng dạng với tam giác
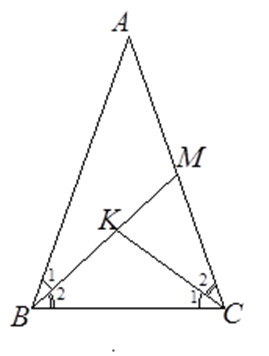
Tam giác $ABC$ cân tại $A$ nên $\widehat {ABC} = \widehat {ACB}$, ta lại có $\widehat {{B_1}} = \widehat {{C_1}}$ (gt) nên $\widehat {{B_2}} = \widehat {{C_2}}$ .
$\Delta MBC$ và $\Delta MCK$có
$\widehat {BMC}$ là góc chung;
$\widehat {{B_2}} = \widehat {{C_2}}$ (chứng minh trên).
Do đó $\Delta MBC\backsim\Delta MCK$ (g.g).
Chọn câu đúng.
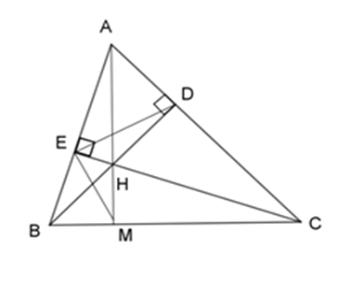
Xét \(\Delta HBE\) và \(\Delta HCD\) có:
\(\widehat {BDC} = \widehat {CEB} = {90^0}\)
\(\widehat {EHB} = \widehat {DHC}\) (2 góc đối đỉnh)
\( \Rightarrow \Delta HBE\backsim\Delta HCD\)(g – g)
Xét \(\Delta ABD\) và \(\Delta ACE\) có
\(\widehat {AEC} = \widehat {BDA} = 90^\circ \)
\(\widehat A\) chung
Nên \(\Delta ABD\backsim\Delta ACE\,\left( {g - g} \right)\).
Tích $BD.CE$ bằng
+ Ta có: \(\widehat {DMC} = \widehat {DME} + \widehat {EMC}\)
Mặt khác: \(\widehat {DMC} = \widehat {ABC} + \widehat {BDM}\) (góc ngoài tam giác)
Mà: \(\widehat {DME} = \widehat {ABC}\)(gt) nên \(\widehat {BDM} = \widehat {EMC}\)
+ Ta có: \(\widehat {ABC} = \widehat {ACB}\) ($\Delta ABC$ cân tại $A$ ) và \(\widehat {BDM} = \widehat {EMC}\) (chứng minh trên)
\( \Rightarrow \)\(\Delta BDM\backsim\Delta CME\;(g - g)\)
\( \Rightarrow \dfrac{{BD}}{{CM}} = \dfrac{{BM}}{{CE}} \Rightarrow BD.CE = CM.BM\)
Lại có M là trung điểm của BC và BC = 2a \( \Rightarrow \)BM = MC = a
\( \Rightarrow BD.CE = {a^2}\) không đổi.
Cho hai tam giác \(ABC\) và \(FED\) có \(\widehat A = \widehat F\), cần thêm điều kiện gì dưới đây để hai tam giác (thứ tự đỉnh như vậy) đồng dạng theo trường hợp góc – góc?
Ta có: \(\widehat A = \widehat F\), \(\widehat B = \widehat E\) thì \(\Delta ABC \backsim \Delta FED\left( {g - g} \right)\).

