Trả lời bởi giáo viên
Đáp án đúng: c
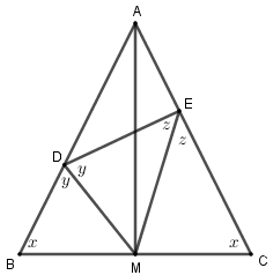
Tam giác \(ABC\) có: \(M\) là trung điểm của \(BC\) nên \(AM\) vừa là đường trung tuyến vừa là đường phân giác trong góc \(A\).
Lại có: \(DM\) là phân giác của góc \(\widehat {BDE}\) nên \(DM\) là phân giác ngoài góc \(D\) của tam giác \(ADE\).
Tam giác \(ADE\) có phân giác trong \(AM\) cắt phân giác ngoài \(DM\) tại \(M\) nên \(EM\) là đường phân giác ngoài góc \(E\) hay \(EM\) là phân giác của góc \(\widehat {DEC}\).
Vậy \(\widehat {DEM} = \widehat {CEM}\).
Hướng dẫn giải:
Sử dụng tính chất đường phân giác ngoài của tam giác: Đường phân giác trong của một góc và các đường phân giác ngoài của hai góc còn lại đồng quy tại một điểm. Điểm này là tâm đường tròn bàng tiếp tam giác.
Câu hỏi khác
- Bài tập định lý Ta-lét. Định lý đảo và hệ quả của định lý Ta-lét toán 8 có lời giải
- Bài tập tính chất đường phân giác của tam giác toán 8 có lời giải
- Bài tập hai tam giác đồng dạng toán 8 có lời giải
- Bài tập trường hợp đồng dạng thứ nhất toán 8 có lời giải
- Bài tập trường hợp đồng dạng thứ hai toán 8 có lời giải
