Câu hỏi:
2 năm trước
Cho tam giác \(ABC\) vuông tại \(A\) có: \(AB = 5,AC = 12\). Trên cạnh \(BC\) lấy điểm \(M\) sao cho \(BM = \dfrac{5}{{13}}BC\). Qua \(M\) kẻ đường thẳng vuông góc với \(AC\) tại \(N\). Độ dài \(MN\) là:
Trả lời bởi giáo viên
Đáp án đúng: c
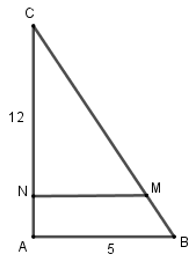
Tam giác \(ABC\) vuông tại \(A\), theo định lí Pi-ta-go ta có:
\(B{C^2} = A{B^2} + A{C^2}\) \( \Rightarrow B{C^2} = {5^2} + {12^2} = 169\) \( \Rightarrow BC = 13\).
\(BM = \dfrac{5}{{13}}BC = \dfrac{5}{{13}}.13 = 5\) \( \Rightarrow CM = 13 - 5 = 8\).
Xét \(\Delta CMN\) và \(\Delta CBA\) có:
\(\widehat N = \widehat A = {90^0}\) (gt)
\(\widehat C\) chung
\( \Rightarrow \Delta CMN \backsim \Delta CBA\left( {g - g} \right)\)\( \Rightarrow \dfrac{{MN}}{{AB}} = \dfrac{{CM}}{{CB}}\) (cạnh tương ứng)
\( \Rightarrow MN = \dfrac{{AB.CM}}{{CB}} = \dfrac{{5.8}}{{13}} = \dfrac{{40}}{{13}}\).
Hướng dẫn giải:
Bước 1: Chứng minh 2 tam giác đồng dạng theo trường hợp góc – góc.
Bước 2: Từ đó ta rút ra được tỉ lệ thức phù hợp, tính ra \(MN\).
Câu hỏi khác
- Bài tập định lý Ta-lét. Định lý đảo và hệ quả của định lý Ta-lét toán 8 có lời giải
- Bài tập tính chất đường phân giác của tam giác toán 8 có lời giải
- Bài tập hai tam giác đồng dạng toán 8 có lời giải
- Bài tập trường hợp đồng dạng thứ nhất toán 8 có lời giải
- Bài tập trường hợp đồng dạng thứ hai toán 8 có lời giải
