Câu hỏi:
2 năm trước
Cho hình bình hành \(ABCD\) có \(I\) là giao điểm của \(AC\) và \(BD\). \(E\) là một điểm bất kì thuộc \(BC\), qua \(E\) kẻ đường thẳng song song với \(AB\) và cắt \(BD,AC,AD\) lại \(G,H,F\). Chọn kết luận sai?
Trả lời bởi giáo viên
Đáp án đúng: a
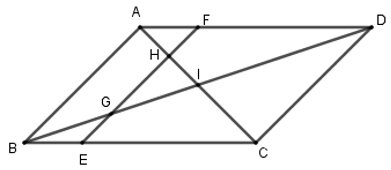
Có \(ABCD\) là hình bình hành nên:
\(AD{\rm{//}}BC, AB{\rm{//}}\,DC\)
Xét \(\Delta BGE\) và \(\Delta DGF\) có:
\(\widehat {BGE} = \widehat {DGF}\) (đối đỉnh)
\(\widehat {EBG} = \widehat {FDG}\) (so le trong)
\( \Rightarrow \Delta BGE \backsim \Delta DGF\) (g-g) nên C đúng.
Xét \(\Delta AHF\) và \(\Delta CHE\) có:
\(\widehat {AHF} = \widehat {CHE}\) (đối đỉnh)
\(\widehat {HAF} = \widehat {HCE}\) (so le trong)
\( \Rightarrow \Delta AHF \backsim \Delta CHE\left( {g - g} \right)\) nên D đúng.
Lại có \(GH//AB\) \( \Rightarrow \widehat {IHG} = \widehat {IAB}\) (đồng vị)
Xét \(\Delta GHI\) và \(\Delta BAI\) có:
Chung \(I\)
\(\widehat {IHG} = \widehat {IAB}\) (cmt)
\( \Rightarrow \Delta GHI \backsim \Delta BAI\left( {g - g} \right)\)
Suy ra B đúng.
Chỉ có A sai.
Hướng dẫn giải:
Tìm dữ kiện cần để chứng minh cặp tam giác đồng dạng theo trường hợp góc – góc.
Câu hỏi khác
- Bài tập định lý Ta-lét. Định lý đảo và hệ quả của định lý Ta-lét toán 8 có lời giải
- Bài tập tính chất đường phân giác của tam giác toán 8 có lời giải
- Bài tập hai tam giác đồng dạng toán 8 có lời giải
- Bài tập trường hợp đồng dạng thứ nhất toán 8 có lời giải
- Bài tập trường hợp đồng dạng thứ hai toán 8 có lời giải
