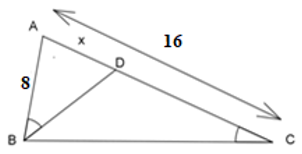
Trả lời bởi giáo viên
Đáp án đúng: c
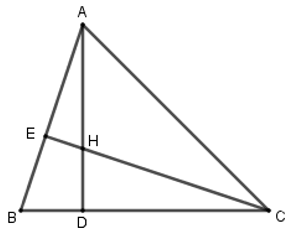
Xét tam giác \(ABD\) và \(CBE\) có:
\(\widehat E = \widehat D = {90^0}\)
Chung \(\widehat B\)
\( \Rightarrow \Delta ABD\backsim\Delta CBE\left( {g - g} \right)\).
\( \Rightarrow \widehat {BAD} = \widehat {BCE} = \widehat {DCH}\) (góc t/ư)
Xét \(\Delta ADB\) và \(\Delta CDH\) có:
\(\begin{array}{l}\widehat {ADB} = \widehat {CDH} = {90^0}\\\widehat {BAD} = \widehat {DCH}\left( {cmt} \right)\end{array}\)
\( \Rightarrow \Delta ADB \backsim \Delta CDH\left( {g - g} \right)\)
Vậy A, B đều đúng.
Hướng dẫn giải:
Chứng minh hai tam giác đồng dạng theo trường hợp góc-góc.
Câu hỏi khác
- Bài tập định lý Ta-lét. Định lý đảo và hệ quả của định lý Ta-lét toán 8 có lời giải
- Bài tập tính chất đường phân giác của tam giác toán 8 có lời giải
- Bài tập hai tam giác đồng dạng toán 8 có lời giải
- Bài tập trường hợp đồng dạng thứ nhất toán 8 có lời giải
- Bài tập trường hợp đồng dạng thứ hai toán 8 có lời giải
