Trả lời bởi giáo viên
Đáp án đúng: c
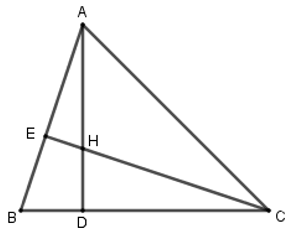
Theo câu a, \Delta ADB \backsim \Delta CDH \Rightarrow \dfrac{{BD}}{{DH}} = \dfrac{{AB}}{{CH}} (cạnh t/ư) nên D đúng.
Xét \Delta AHE và \Delta CHD có:
\widehat {AHE} = \widehat {CHD} (đối đỉnh)
\widehat {EAH} = \widehat {DCH}\left( {cmt} \right)
Suy ra \Delta AHE \backsim \Delta CHD\left( {g - g} \right) \Rightarrow \dfrac{{HA}}{{HC}} = \dfrac{{HE}}{{HD}} (cạnh t/ư) \Rightarrow \dfrac{{HA}}{{HE}} = \dfrac{{HC}}{{HD}}.
Xét \Delta HAC và \Delta HED có:
\widehat {AHC} = \widehat {EHD} (đối đỉnh)
\dfrac{{HA}}{{HE}} = \dfrac{{HC}}{{HD}}\left( {cmt} \right)
Suy ra \Delta HAC \backsim \Delta HED(c-g-c)
\Rightarrow \widehat {HCA} = \widehat {HDE} (góc t/ư) hay C sai.
Hướng dẫn giải:
Chứng minh các cặp tam giác đồng dạng, từ đó rút ra dữ kiện cần thiết để chứng minh yêu cầu của bài toán.
Câu hỏi khác
- Bài tập định lý Ta-lét. Định lý đảo và hệ quả của định lý Ta-lét toán 8 có lời giải
- Bài tập tính chất đường phân giác của tam giác toán 8 có lời giải
- Bài tập trường hợp đồng dạng thứ nhất toán 8 có lời giải
- Bài tập hai tam giác đồng dạng toán 8 có lời giải
- Bài tập trường hợp đồng dạng thứ hai toán 8 có lời giải
