Câu hỏi:
2 năm trước
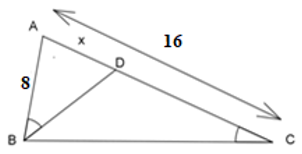
Tam giác \(ABC\) có: \(\widehat A = 2\widehat B\), \(AC = 16\,{\rm{cm}}\), \(BC = 20\,{\rm{cm}}\). Tính độ dài cạnh \(AB\).
Trả lời bởi giáo viên
Đáp án đúng: d
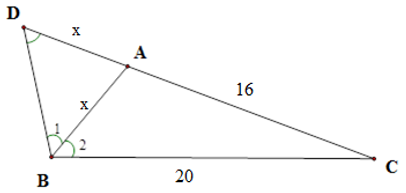
Trên tia đối của tia \(AC\) lấy điểm \(D\) sao cho \(AD = AB = x\).
Tam giác \(ABD\) cân tại \(A\) nên \(\widehat {BAC} = \widehat {{B_1}} + \widehat D = 2\widehat D\).
Ta lại có: \(\widehat {BAC} = 2\widehat {{B_2}}\) nên \(\widehat D = \widehat {{B_2}}\).
Xét \(\Delta CBA\) và \(\Delta CDB\) có: \(\widehat C\) chung và \(\widehat D = \widehat {{B_2}}\)
Nên \(\Delta CBA\backsim\Delta CDB\,\left( {g - g} \right)\) nên \(\dfrac{{CB}}{{CD}} = \dfrac{{AC}}{{BC}}\),
tức là \(\dfrac{{20}}{{16 + x}} = \dfrac{{16}}{{20}}\)\( \Leftrightarrow 16 + x = \dfrac{{20.20}}{{16}} = 25\) \( \Rightarrow x = 25 - 16 = 9\left( {cm} \right)\).
Vậy \(AB = 9cm\).
Hướng dẫn giải:
Bước 1: Trên tia đối của tia \(AC\) lấy điểm \(D\) sao cho \(AD = AB\)
Bước 2: Tìm dữ kiện cần để chứng minh cặp tam giác đồng dạng theo trường hợp góc – góc.
Bước 3: Từ tam giác đồng dạng suy ra tỉ lệ cạnh thích hợp để tính \(AB\).
Câu hỏi khác
- Bài tập định lý Ta-lét. Định lý đảo và hệ quả của định lý Ta-lét toán 8 có lời giải
- Bài tập tính chất đường phân giác của tam giác toán 8 có lời giải
- Bài tập hai tam giác đồng dạng toán 8 có lời giải
- Bài tập trường hợp đồng dạng thứ nhất toán 8 có lời giải
- Bài tập trường hợp đồng dạng thứ hai toán 8 có lời giải
