Câu hỏi:
2 năm trước
Cho tam giác \(ABC\) có \(\widehat A = {70^0}\). Gọi \(I\) là giao điểm các tia phân giác \(\widehat B\) và \(\widehat C\). Số đo \(\widehat {BIC}\) là:
Trả lời bởi giáo viên
Đáp án đúng: c
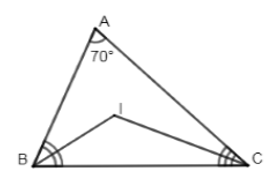
Vì \(BI\) và \(CI\) là tia phân giác của \(\angle ABC\) và \(\angle ACB\,\,\left( {gt} \right)\)
\( \Rightarrow \left\{ \begin{array}{l}\angle IBC = \dfrac{1}{2}\angle ABC\\\angle ICB = \dfrac{1}{2}\angle ACB\end{array} \right.\) (tính chất tia phân giác)
\( \Rightarrow \angle IBC + \angle ICB = \dfrac{1}{2}\left( {\angle ABC + \angle ACB} \right) = \dfrac{1}{2}\left( {{{180}^0} - \angle A} \right) = \dfrac{1}{2}\left( {{{180}^0} - {{70}^0}} \right) = \dfrac{1}{2}{.110^0} = {55^0}\)
Xét \(\Delta BIC\) có: \(\angle BIC + \angle IBC + \angle ICB = {180^0}\) (tổng ba góc trong tam giác)
\( \Rightarrow \angle BIC = {180^0} - \left( {\angle IBC + \angle ICB} \right) = {180^0} - {55^0} = {125^0}\).
Hướng dẫn giải:
Áp dụng tính chất tia phân giác và định lý: Tổng ba góc trong tam giác bằng \(180^0.\)
Câu hỏi khác
- Đề thi khảo sát chất lượng đầu năm - Đề số 1 toán 8 có lời giải
- Đề thi khảo sát chất lượng đầu năm - Đề số 2 toán 8 có lời giải
- Đề thi khảo sát chất lượng đầu năm - Đề số 3 toán 8 có lời giải
- Đề thi khảo sát chất lượng đầu năm - Đề số 5 toán 8 có lời giải
- Đề thi khảo sát chất lượng đầu năm - Đề số 4 toán 8 có lời giải
