Câu hỏi:
2 năm trước
Cho \(\Delta ABC\) có \(AB = AC\), \(\widehat A = 2\widehat B\) có dạng đặc biệt nào:
Trả lời bởi giáo viên
Đáp án đúng: d
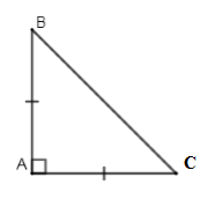
Vì \(AB = AC\,\left( {gt} \right) \Rightarrow \Delta ABC\) cân tại \(A\) (dấu hiệu nhận biết tam giác cân)
\( \Rightarrow \angle B = \angle C\) (tính chất tam giác cân).
Ta có: \(\angle A + \angle B + \angle C = {180^0}\) (định lý tổng ba góc của tam giác).
Mà \(\left\{ \begin{array}{l}\angle B = \angle C\\\angle A = 2\angle B\\\angle A + \angle B + \angle C = {180^0}\end{array} \right. \\\Rightarrow 2\angle B + 2\angle C = {180^0} \\\Rightarrow \angle B + \angle C = {180^0}:2 = {90^0}\\ \Rightarrow \angle A = {180^0} - {90^0} = {90^0}\)
\( \Rightarrow \Delta ABC\) là tam giác vuông cân tại \(A\) (dấu hiệu nhận biết tam giác vuông cân).
Hướng dẫn giải:
Áp dụng định lý tổng ba góc trong tam giác, tính chất tam giác cân, dấu hiệu nhận biết tam giác vuông cân.
Câu hỏi khác
- Đề thi khảo sát chất lượng đầu năm - Đề số 1 toán 8 có lời giải
- Đề thi khảo sát chất lượng đầu năm - Đề số 2 toán 8 có lời giải
- Đề thi khảo sát chất lượng đầu năm - Đề số 3 toán 8 có lời giải
- Đề thi khảo sát chất lượng đầu năm - Đề số 5 toán 8 có lời giải
- Đề thi khảo sát chất lượng đầu năm - Đề số 4 toán 8 có lời giải
