Cho tam giác \(ABC\), lấy \(M\) thuộc \(BC\) sao cho \(BM = 3CM\). Hãy chọn câu sai:
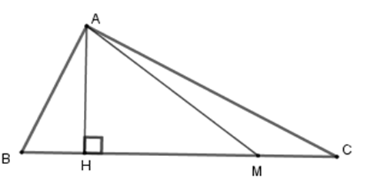
Kẻ \(AH \bot BC\) tại \(H\) .
Mà \(BM = 3CM\)\( \Rightarrow BM = \dfrac{3}{4}BC;\,CM = \dfrac{1}{4}BC;\,\)
Khi đó ta có
\(\begin{array}{l}{S_{ABM}} = \dfrac{1}{2}.\,AH.BM = \dfrac{1}{2}AH.\dfrac{3}{4}BC\\ = \dfrac{3}{4}.\left( {\dfrac{1}{2}AH.BC} \right) = \dfrac{3}{4}{S_{ABC}}\end{array}\)
Suy ra A đúng.
\(\begin{array}{l}{S_{AMB}} = \dfrac{1}{2}.\,AH.MB = \dfrac{1}{2}AH.3MC\\ = 3.\left( {\dfrac{1}{2}AH.MC} \right) = 3{S_{AMC}}\end{array}\)
Suy ra B đúng.
\(\begin{array}{l}{S_{ABC}} = \dfrac{1}{2}.\,AH.BC = \dfrac{1}{2}AH.4MC = 4{S_{AMC}}\\ \Rightarrow {S_{ABC}} = 4{S_{AMC}} \Leftrightarrow {S_{AMC}} = \dfrac{1}{4}{S_{ABC}}\end{array}\)
suy ra D đúng, C sai.
Cho tam giác \(ABC\), \(AM\) là đường trung tuyến. Biết diện tích của \(\Delta ABC\) bằng \(60\,c{m^2}\). Diện tích của tam giác \(AMC\) là:
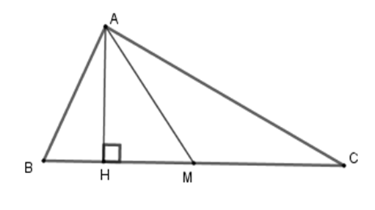
Kẻ \(AH \bot BC\) tại \(H\) .
Ta có \({S_{ABC}} = \dfrac{1}{2}AH.BC;\,{S_{AMC}} = \dfrac{1}{2}AH.MC\)
Mà \(AM\) là đường trung tuyến nên \(M\) là trung điểm của \(BC\)\( \Rightarrow BC = 2AM\)
Từ đó \({S_{ABC}} = \dfrac{1}{2}AH.BC = \dfrac{1}{2}AH.2MC = 2{S_{AMC}}\)
Suy ra \({S_{AMC}} = \dfrac{1}{2}{S_{ABC}} = \dfrac{1}{2}.60 = 30\,c{m^2}\) .
Vậy \({S_{AMC}} = 30\,c{m^2}\) .
Cho tam giác $ABC$ vuông tại $A$ , biết \(BC = 5\,cm;AC = 3cm\). Diện tích tam giác \(ABC\) là:
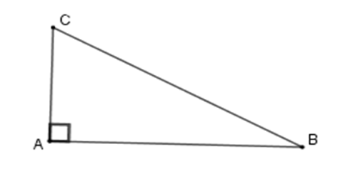
+ Áp dụng định lý Pytago cho tam giác vuông \(ABC\) ta có
\(\begin{array}{l}B{C^2} = A{C^2} + A{B^2}\\ \Rightarrow A{B^2} = {5^2} - {3^2}\\ \Rightarrow A{B^2} = 16 \Rightarrow AB = 4\,cm\end{array}\)
+ Suy ra \({S_{ABC}} = \dfrac{{AC.AB}}{2} = \dfrac{{3.4}}{2} = 6\,c{m^2}\) .
Tam giác $ABC$ vuông tại $A$ , vẽ hình chữ nhật $ABDC$ . Biết diện tích của tam giác vuông là \(140\,c{m^2}\). Diện tích hình chữ nhật $ABDC$ là:
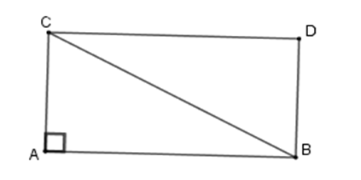
Vì \(ABDC\) là hình chữ nhật nên \({S_{ABDC}} = AC.AB\) mà \({S_{ABC}} = \dfrac{{AC.AB}}{2}\)
Nên \({S_{ABDC}} = 2{S_{ABC}} = 2.140 = 280\,c{m^2}\) .
Cho tứ giác$ABCD$ có hai đường chéo vuông góc với nhau. Gọi $E,F,G,H$ lần lượt là trung điểm các cạnh$AB,BC,CD,DA$ . Biết diện tích của tứ giác $ABCD$ là \(18\,{m^2}\) thì diện tích của tứ giác $EFGH$ là:
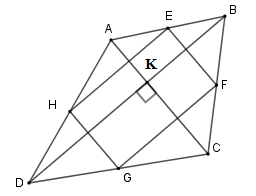
+ Vì $E,F,G,H$ lần lượt là trung điểm các cạnh$AB,BC,CD,DA$ nên \(EF;\,FG;\,GH;\,HE\) lần lượt là đường trung bình của các tam giác \(ABC;\,BCD;\,ADC;\,ADB\)
nên \(EF{\rm{//}}HG\) (vì cùng song song với \(AC\) ); \(HE{\rm{//}}FG\,\)( vì cùng song song với \(BD\) )
Suy ra tứ giác \(EFGH\) là hình bình hành, mà \(AC \bot BD\,\left( {gt} \right) \Rightarrow EFGH\) là hình chữ nhật.
Do đó \({S_{EFGH}} = HE.EF\) , mà \(EF = \dfrac{1}{2}AC;\,HE = \dfrac{1}{2}BD\) (tính chất đường trung bình)
Nên \({S_{EFGH}} = \dfrac{1}{2}AC.\dfrac{1}{2}BD \)\(= \dfrac{1}{4}AC.BD.\)
+ Gọi \(K\) là giao của \(AC\) và \(BD\).
Khi đó
\(\begin{array}{l}{S_{ABCD}} = {S_{ABC}} + {S_{ACD}}\\ = \dfrac{1}{2}BK.AC + \dfrac{1}{2}DK.AC\\ = \dfrac{1}{2}AC\left( {BK + DK} \right)\\ = \dfrac{1}{2}AC.BD\end{array}\)
Mà \({S_{ABCD}} = 18\,{m^2} \Rightarrow \dfrac{1}{2}AC.BD = 18 \Rightarrow AC.BD = 36\,{m^2}.\)
Suy ra \({S_{EFGH}} = \dfrac{1}{4}AC.BD \)\(= \dfrac{1}{4}.36 = 9\,{m^2}.\)
Một hình chữ nhật có diện tích là $24\,c{m^2}$, chiều dài là $8\,cm$. Chu vi hình chữ nhật đó là
Gọi chiều rộng hình chữ nhật là \(a\) , ta có $S = a.8 \Leftrightarrow 8a = 24 \Leftrightarrow a = 3\,cm$ .
Chu vi hình chữ nhật là \(S = \left( {3 + 8} \right).2 = 22\,cm\) .
Cho tam giác $ABC$ có diện tích \(12\,c{m^2}\) . Gọi $N$ là trung điểm của$BC$ , $M$ trên $AC$ sao cho \(AM = \dfrac{1}{3}AC\) , $AN$ cắt $BM$ tại $O$ .
Khẳng định nào sau đây là đúng nhất?
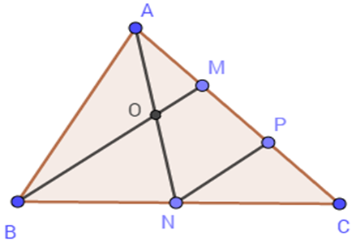
+ Lấy $P$ là trung điểm của$CM$ .
Tam giác BCM có: \(\left\{ \begin{array}{l}NB = NC\,\,(gt)\\PC = PM\,\,(gt)\end{array} \right.\)
Suy ra $NP$ là đường trung bình của tam giác $BMC$ (định nghĩa).
Suy ra \(NP{\rm{//}}BM\) (tính chất đường trung bình).
Tam giác $ANP$ có \(\left\{ \begin{array}{l}MA = MP\,\,\,(gt)\\OM{\rm{//}}NP\,\,\,({\rm{do}}\,\,NP{\rm{//}}BM)\end{array} \right.\)
\( \Rightarrow AO = ON\) (định lý đảo của đường trung bình) .
+ Ta có $OM$ là đường trung bình của tam giác $ANP$ (cmt) nên \(OM = \dfrac{1}{2}NP\,\,\,\,(1)\)
$NP$ là đường trung bình của tam giác $BCM$ nên \(NP = \dfrac{1}{2}BM\,\,\,(2)\)
Từ (1) và (2) suy ra \(BM = 4OM \Rightarrow BO = 3OM\) .
Vậy \(AO = ON;\,BO = 3OM\) .
Cho tam giác $ABC$ có diện tích \(12\,c{m^2}\) . Gọi $N$ là trung điểm của$BC$ , $M$ trên $AC$ sao cho \(AM = \dfrac{1}{3}AC\) , $AN$ cắt $BM$ tại $O$ .
Tính diện tích tam giác AOM
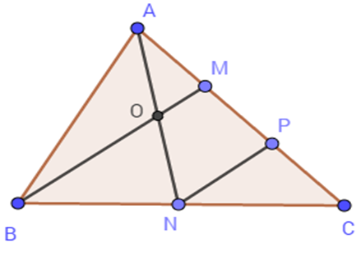
Hai tam giác $AOM$ và $ABM$ có chung đường cao hạ từ $A$ nên \(\dfrac{{{S_{AOM}}}}{{{S_{ABM}}}} = \dfrac{{OM}}{{BM}} = \dfrac{1}{4} \Rightarrow {S_{AOM}} = \dfrac{1}{4}{S_{ABM}}\)
Hai tam giác $ABM$ và $ABC$ có chung đường cao hạ từ $B$ nên \(\dfrac{{{S_{ABM}}}}{{{S_{ABC}}}} = \dfrac{{AM}}{{AC}} = \dfrac{1}{3} \Rightarrow {S_{ABM}} = \dfrac{1}{3}{S_{ABC}}\)
Vậy \({S_{AOM}} = \dfrac{1}{4}.\dfrac{1}{3}.12 = 1\left( {c{m^2}} \right)\)
Cho hình bình hành ABCD. Đường phân giác của các góc A và C cắt đường chéo BD tại E và F.
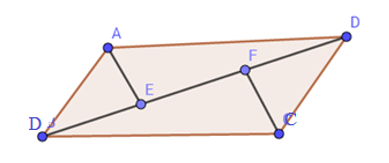
Ta có: \(\left\{ \begin{array}{l}{S_{ABCFE}} = {S_{ABE}} + {S_{BFC}}\\{S_{ADCFE}} = {S_{DFC}} + {S_{DAE}}\end{array} \right.\)
Xét hình hình hành ABCD có AE và CF lần lượt là phân giác cảu các góc A và C nên suy ra:
\(\widehat {BAE} = \widehat {DAE} = \widehat {BCF} = \widehat {DCF}\).
Xét \(\Delta ABE\) và \(\Delta CDF\) có:
\(\begin{array}{l}AB = CD\,\,(gt)\\\widehat {ABE} = \widehat {CDF}\,\,\,(slt)\\\widehat {BAE} = \widehat {DCF}\,\,(cmt)\\ \Rightarrow \Delta ABE = \Delta CDF\,\,(g.c.g)\\ \Rightarrow {S_{ABE}} = {S_{CDF}} \,\,(1)\end{array}\).
Xét \(\Delta BCF\) và \(\Delta DAE\) có:
\(\begin{array}{l}AD = BC\,\,(gt)\\\widehat {ADE} = \widehat {CBF\,\,}(slt)\\\widehat {DAE} = \widehat {BCF}\,\,(cmt)\end{array}\).
\(\begin{array}{l} \Rightarrow \Delta BCF = \Delta DAE\,\,(g.c.g)\\ \Rightarrow {S_{BCF}} = {S_{DAE}} \,\,(2)\end{array}\).
Từ (1) và (2) suy ra:
\({S_{ABE}} + {S_{BCF}} = {S_{CDF}} + {S_{DAE}} \Rightarrow {S_{ABCFE}} = {S_{ADCFE}}\).
Cho tam giác \(ABC\) vuông cân tại \(A.\) Dựng về phía ngoài tam giác các hình vuông \(ABMN,ACDE,\,BCHK\). Chọn câu đúng.
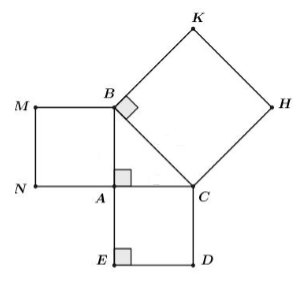
Giả sử tam giác ABC vuông cân tại A có \(AB = AC = a.\)
Áp dụng định lý Pi-ta-go ta có: \(B{C^2} = A{B^2} + A{C^2} = {a^2} + {a^2} = 2{a^2}\).
Ta có: \(\left\{ \begin{array}{l}{S_{ABCD}} = A{C^2} = {a^2}\\{S_{ABMN}} = A{B^2} = {a^2}\\{S_{BCHK}} = B{C^2} = 2{a^2}\end{array} \right.\)
\( \Rightarrow {S_{DCHK}} = {S_{ACDE}} + {S_{ABMN}}.\)
Trong các hình chữ nhật có cùng chu vi \(100cm,\) hình có diện tích lớn nhất là bao nhiêu?
Nửa chu vi của hình chữ nhật là \(100:2 = 50cm\).
Gọi một kích thước của hình chữ nhật là \(x\,\,\left( {cm;x > 0} \right)\) thì kích thước còn lại là \(50 - x\,\,\left( {cm} \right)\).
Diện tích hình chữ nhật bằng \(x\left( {50 - x} \right) = - {x^2} + 50x = - \left( {{x^2} - 50x + 625} \right) + 625\)\( = 625 - {\left( {x - 25} \right)^2}\).
Ta có: \({\left( {x - 25} \right)^2} \ge 0;\forall x \Leftrightarrow 625 - {\left( {x - 25} \right)^2} \le 625;\,\forall x\).
Dấu “=” xảy ra khi \(x = 25\).
Vậy hình chữ nhật có diện tích lớn nhất là \(625\,c{m^2}.\)
Tính chu vi một tam giác vuông có cạnh huyền bằng \(26\,cm\), hiệu hai cạnh góc vuông bằng \(14\,cm.\)
Gọi 1 cạnh góc vuông là \(x\left( {cm;x > 0} \right)\).
Thì cạnh góc vuông còn lại là \(\left( {x + 14} \right)\,cm\).
Theo định lý Pytago ta có: \({x^2} + {\left( {x + 14} \right)^2} = {26^2}\).
\( \Leftrightarrow {x^2} + {x^2} + 28x + {14^2} = {26^2}\).
\( \Leftrightarrow 2{x^2} + 28x - 480 = 0\)
\( \Leftrightarrow {x^2} + 14x - 240 = 0\)
\(\begin{array}{l} \Leftrightarrow {x^2} + 24x - 10x - 240 = 0\\ \Leftrightarrow x\left( {x + 24} \right) - 10\left( {x + 24} \right) = 0\\ \Leftrightarrow \left( {x - 10} \right)\left( {x + 24} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 10 = 0\\x + 24 = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = 10\left( {tm} \right)\\x = - 24\left( {ktm} \right)\end{array} \right.\end{array}\).
Suy ra hai cạnh góc vuông của tam giác là \(10\,cm;\,10 + 14 = 24\,cm\).
Chu vi tam giác vuông là \(10 + 24 + 26 = 60\,cm\).

