Cho hình bình hành ABCD. Đường phân giác của các góc A và C cắt đường chéo BD tại E và F.

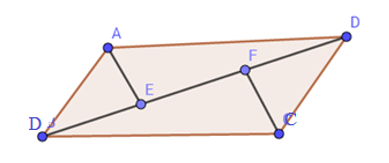
Ta có: \(\left\{ \begin{array}{l}{S_{ABCFE}} = {S_{ABE}} + {S_{BFC}}\\{S_{ADCFE}} = {S_{DFC}} + {S_{DAE}}\end{array} \right.\)

Xét hình hình hành ABCD có AE và CF lần lượt là phân giác cảu các góc A và C nên suy ra:

\(\widehat {BAE} = \widehat {DAE} = \widehat {BCF} = \widehat {DCF}\).

Xét \(\Delta ABE\) và \(\Delta CDF\) có:

\(\begin{array}{l}AB = CD\,\,(gt)\\\widehat {ABE} = \widehat {CDF}\,\,\,(slt)\\\widehat {BAE} = \widehat {DCF}\,\,(cmt)\\ \Rightarrow \Delta ABE = \Delta CDF\,\,(g.c.g)\\ \Rightarrow {S_{ABE}} = {S_{CDF}}  \,\,(1)\end{array}\).

Xét \(\Delta BCF\) và \(\Delta DAE\) có:

\(\begin{array}{l}AD = BC\,\,(gt)\\\widehat {ADE} = \widehat {CBF\,\,}(slt)\\\widehat {DAE} = \widehat {BCF}\,\,(cmt)\end{array}\).

\(\begin{array}{l} \Rightarrow \Delta BCF = \Delta DAE\,\,(g.c.g)\\ \Rightarrow {S_{BCF}} = {S_{DAE}}  \,\,(2)\end{array}\).

Từ (1) và (2) suy ra:

\({S_{ABE}} + {S_{BCF}} = {S_{CDF}} + {S_{DAE}} \Rightarrow {S_{ABCFE}} = {S_{ADCFE}}\).