Câu hỏi:
2 năm trước
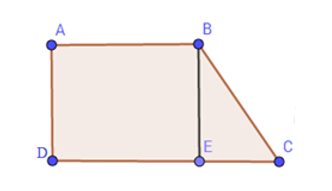
Tính diện tích mảnh đất hình thang vuông \(ABCD\) có độ dài hai đáy \(AB = 9\,cm;\,DC = 13,5\,cm;\,\widehat A = \widehat D = 90^\circ \) ( hình vẽ), biết tam giác \(BEC\) vuông tại \(E\) và có diện tích bằng \(18\,c{m^2}\).
Trả lời bởi giáo viên
Đáp án đúng: c
Tứ giác \(ABED\) có \(\widehat A = \widehat D = \widehat E = 90^\circ \) nên là hình chữ nhật.
Suy ra \(DE = AB = 9\,cm\). Do đó: \(EC = DC - DE = 13,5 - 9 = 4,5\,(cm)\)
Ta có:
\({S_{BEC}} = \dfrac{1}{2}BE.EC \Rightarrow BE = \dfrac{{2{S_{BEC}}}}{{EC}} = \dfrac{{2.18}}{{4,5}} = 8\,(cm)\).
\({S_{ABED}} = AB.BE = 9. 8 = 72\,\,\left( {c{m^2}} \right)\).
\({S_{ABCD}} = {S_{ABED}} + {S_{BEC}} = 72 + 18 = 90\,(c{m^2})\).
Hướng dẫn giải:
Sử dụng:
Công thức tính diện tích hình chữ nhật \(S = ab\).
Công thức tính diện tích hình tam giác vuông \(S = \dfrac{{ab}}{2}\).
