Câu hỏi:
2 năm trước
Cho hình thoi có cạnh là \(10\,cm\), một trong hai đường chéo có độ dài là \(16\,cm\). Diện tích của hình thoi là:
Trả lời bởi giáo viên
Đáp án đúng: c
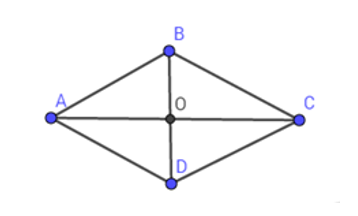
Giả sử hình thoi \(ABCD\), đường chéo \(AC\) vuông góc với \(BD\) tại \(O\), \(AB = 10\,cm;\,\,\,AC = 16\,cm.\)
\(AO = \dfrac{1}{2}AC = \dfrac{1}{2}. 16 = 8\,(cm)\).
Áp dụng định lí Py-ta-go trong tam giác vuông \(AOB\) vuông tại \(O\) ta có:
\(OB = \sqrt {A{B^2} - O{A^2}} = \sqrt {{{10}^2} - {8^2}} = 6\).
\({S_{ABCD}} = \dfrac{1}{2}BD. AC = \dfrac{1}{2}. 2OB. AC\) \( = OB. AC = 6. 16 = 96\left( {c{m^2}} \right)\).
Hướng dẫn giải:
Tính \(BO,AO\) (sử dụng định lí Py-ta-go).
Sau đó thay vào công thức tính diện tích hình thoi \(S = \dfrac{{{d_1}{d_2}}}{2}\) với \({d_1};{d_2}\) là độ dài hai đường chéo.

