Câu hỏi:
2 năm trước
Hình thoi có độ dài hai đường chéo là \(15\,cm\) và \(20\,cm\). Tính độ dài đường cao của hình thoi.
Trả lời bởi giáo viên
Đáp án đúng: a
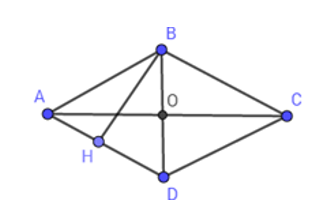
Giả sử hình thoi \(ABCD\), đường chéo \(AC\) vuông góc với \(BD\) tại \(O\), \(AC = 20\,cm;\,BD = 15\,cm\).
Gọi \(BH\) là đường cao hình thoi kẻ từ đỉnh \(B\).
Ta có: \(DO = \dfrac{1}{2}BD = \dfrac{1}{2}.15 = 7,5\,(cm);\,\)\(AO = \dfrac{1}{2}AC = \dfrac{1}{2}.20 = 10\,(cm)\).
Áp dụng định lí Py-ta-go trong tam giác vuông \(AOD\) vuông tại \(O\) ta có:
\(\begin{array}{l}AD = \sqrt {A{O^2} + O{D^2}} = \sqrt {{{10}^2} + 7,{5^2}} = 12,5\,(cm)\\{S_{ABCD}} = \dfrac{1}{2}BD.AC = \dfrac{1}{2}.15.20 = 150\left( {c{m^2}} \right)\\{S_{ABCD}} = BH.AD\\ \Rightarrow BH = \dfrac{{{S_{ABCD}}}}{{AD}} = \dfrac{{150}}{{12,5}} = 12\,(cm).\end{array}\).
Hướng dẫn giải:
Tính cạnh của hình thoi sử dụng định lí Py-ta-go.
Từ công thức tính diện tích hình thoi bằng tích của cạnh với đường cao tương ứng ta suy ra độ dài đường cao hình thoi.
