Trả lời bởi giáo viên
Đáp án đúng: b
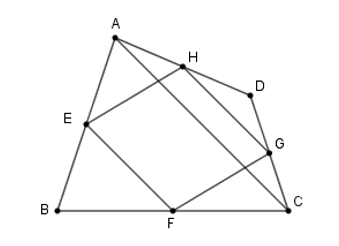
Theo kết quả câu trước ta có: \({S_{BEF}} = \dfrac{1}{4}{S_{ABC}}\).
Chứng minh tương tự ta có: \({S_{DHG}} = \dfrac{1}{4}{S_{DAC}};\,{S_{AEH}} = \dfrac{1}{4}{S_{ABD}};\,{S_{CDF}} = \dfrac{1}{4}{S_{CDB}}\).
Từ đó ta có: \({S_{BEF}} + {S_{DHG}} = \dfrac{1}{4}{S_{BAC}} + \dfrac{1}{4}{S_{DAC}}\)\( = \dfrac{1}{4}\left( {{S_{BAC}} + {S_{DAC}}} \right) = \dfrac{1}{4}{S_{ABCD}} = \dfrac{1}{4}S\).
Và \({S_{AEH}} + {S_{CGF}} = \dfrac{1}{4}{S_{BAD}} + \dfrac{1}{4}{S_{DBC}}\)\( = \dfrac{1}{4}\left( {{S_{BAD}} + {S_{DBC}}} \right) = \dfrac{1}{4}{S_{ABCD}} = \dfrac{1}{4}S\).
Suy ra: \({S_{AEH}} + {S_{CGF}} + {S_{BEF}} + {S_{CFG}} = \dfrac{1}{4}S + \dfrac{1}{4}S = \dfrac{1}{2}S\).
Từ đó: \({S_{EFGH}} = {S_{ABCD}} - \left( {{S_{AEH}} + {S_{CGF}} + {S_{BEF}} + {S_{CFG}}} \right) = S - \dfrac{1}{2}S = \dfrac{1}{2}S\).
