Phương trình \(\left| {x - 1} \right| + \left| {x - 3} \right| = 2x - 1\) có số nghiệm là
Đặt \(\left| {x - 1} \right| + \left| {x - 3} \right| = 2x - 1\;\;\;\left( 1 \right)\)
Xét: \(\begin{array}{l} + )\;\;x - 1 = 0 \Leftrightarrow x = 1\\ + )\;\;x - 3 = 0 \Leftrightarrow x = 3.\end{array}\)
Ta có bảng xét dấu đa thức $x - 1$ và $x - 3$ dưới đây
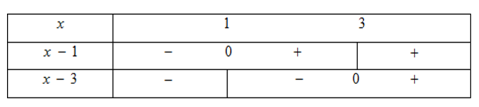
+) Xét khoảng \(x < 1\) ta có:
\((1) \Leftrightarrow (1 - x) + (3 - x) = 2x - 1 \Leftrightarrow - 2x + 4 = 2x - 1 \Leftrightarrow 4x = 5 \Leftrightarrow x = \dfrac{5}{4}\) (Không thuộc khoảng đang xét)
+) Xét khoảng \(1 \le x \le 3\) ta có
\((1) \Leftrightarrow (x - 1) + (3 - x) = 2x - 1 \Leftrightarrow 2 = 2x - 1 \Leftrightarrow x = \dfrac{3}{2}(TM)\)
+) Xét khoảng \(x > 3\) ta có:
\((1) \Leftrightarrow (x - 1) + (x - 3) = 2x - 1 \Leftrightarrow 0.x = - 3\) (phương trình vô nghiệm)
Vậy phương trình có nghiệm \(x = \dfrac{3}{2}\).
Nghiệm của bất phương trình \(\dfrac{{x + 4}}{{x + 1}} + \dfrac{x}{{x - 1}} < \dfrac{{2{x^2}}}{{{x^2} - 1}}\) là
\(\begin{array}{l}\;\dfrac{{x + 4}}{{x + 1}} + \dfrac{x}{{x - 1}} < \dfrac{{2{x^2}}}{{{x^2} - 1}}\\ \Leftrightarrow \;\dfrac{{x + 4}}{{x + 1}} + \dfrac{x}{{x - 1}} < \dfrac{{2{x^2}}}{{\left( {x - 1} \right)\left( {x + 1} \right)}}\;\;\;\left( * \right)\end{array}\)
Điều kiện \(\left\{ \begin{array}{l}x - 1 \ne 0\\x + 1 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ne 1\\x \ne - 1\end{array} \right..\)
\(\left( * \right) \Leftrightarrow \dfrac{{\left( {x + 4} \right)\left( {x - 1} \right)}}{{\left( {x - 1} \right)\left( {x + 1} \right)}} + \dfrac{{x\left( {x + 1} \right)}}{{\left( {x - 1} \right)\left( {x + 1} \right)}} < \dfrac{{2{x^2}}}{{\left( {x + 1} \right)\left( {x - 1} \right)}}\)\( \Leftrightarrow \dfrac{{{x^2} + 3x - 4 + {x^2} + x - 2{x^2}}}{{\left( {x - 1} \right)\left( {x + 1} \right)}} < 0\)
\( \Leftrightarrow \dfrac{{4x - 4}}{{\left( {x - 1} \right)\left( {x + 1} \right)}} < 0\)\( \Leftrightarrow \dfrac{{4\left( {x - 1} \right)}}{{\left( {x - 1} \right)\left( {x + 1} \right)}} < 0 \Leftrightarrow \dfrac{4}{{x + 1}} < 0\) mà \(4 > 0\) nên \(x + 1 < 0 \Leftrightarrow x < - 1.\)
Kết hợp với điều kiện ta có bất phương trình có nghiệm \(x < - 1\).
Tập nghiệm của các bất phương trình ${x^2} + 2(x - 3) - 1 > x(x + 5) + 5$ và $\dfrac{2}{3} - \dfrac{{3x - 6}}{2} > \dfrac{{1 + 3x}}{6}$ lần lượt là
$\begin{array}{l} + )\;\;{x^2} + 2(x - 3) - 1 > x(x + 5) + 5\\ \Leftrightarrow {x^2} + 2x - 6 - 1 > {x^2} + 5x + 5\\ \Leftrightarrow {x^2} + 2x - {x^2} - 5x > 5 + 6 + 1\\ \Leftrightarrow - 3x > 12\\ \Leftrightarrow x < - 4\end{array}$
Vậy tập nghiệm của bất phương trình trên là: \({S_1} = \left\{ {x/x < - 4} \right\}\)
\(\begin{array}{l} + )\;\;\dfrac{2}{3} - \dfrac{{3x - 6}}{2} > \dfrac{{1 + 3x}}{6}\\ \Leftrightarrow 2.2 - 3(3x - 6) > 1 + 3x\\ \Leftrightarrow 4 - 9x + 18 > 1 + 3x\\ \Leftrightarrow 12x < 21 \Leftrightarrow x < \dfrac{7}{4}\end{array}\)
Vậy tập nghiệm của bất phương trình là \({S_1} = \left\{ {x/x < \dfrac{7}{4}} \right\}\)
Tích các nghiệm của phương trình $|{x^2} + 2x - 1| = 2$ là
\(\;\;\left| {{x^2} + 2x - 1} \right| = 2 \Leftrightarrow \left[ \begin{array}{l}{x^2} + 2x - 1 = 2\\{x^2} + 2x - 1 = - 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}{x^2} + 2x - 3 = 0\\{x^2} + 2x + 1 = 0\end{array} \right.\)
\( \Leftrightarrow \left[ \begin{array}{l}{x^2} + 3x - x - 3 = 0\\{(x + 1)^2} = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x(x + 3) - (x + 3) = 0\\x + 1 = 0\end{array} \right.\)
\( \Leftrightarrow \left[ \begin{array}{l}(x + 3)(x - 1) = 0\\x = - 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x + 3 = 0\\x - 1 = 0\\x = - 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - 3\\x = 1\\x = - 1\end{array} \right..\)
Vậy nghiệm của phương trình là $x{\rm{ }} = - 3;{\rm{ }}x = \pm 1.$
Tích các nghiệm của phương trình là \(\left( { - 3} \right).1.\left( { - 1} \right) = 3.\)
Chọn câu đúng, biết \(0 < a < b.\)
Với \(0 < a < b\) ta có \({\left( {a - b} \right)^2} > 0\)
\( \Leftrightarrow {a^2} + {b^2} > 2ab \Leftrightarrow \dfrac{{{a^2}}}{{ab}} + \dfrac{{{b^2}}}{{ab}} > 2\,\,\left( {{\rm{do}}\,ab > 0} \right)\)
\( \Leftrightarrow \dfrac{a}{b} + \dfrac{b}{a} > 2.\)
Vậy với mọi \(0 < a < b\) ta luôn có \(\dfrac{a}{b} + \dfrac{b}{a} > 2.\)
Cho số thực \(x\) , chọn câu đúng nhất.
+) Đáp án A: Bất đẳng thức tương đương với \({x^4} - 4x + 3 \ge 0\)
\(\begin{array}{l} \Leftrightarrow \left( {x - 1} \right)\left( {{x^3} + {x^2} + x - 3} \right) \ge 0 \\\Leftrightarrow \left( {x - 1} \right)\left( {\left( {{x^3} - 1} \right) + \left( {{x^2} + x - 2} \right)} \right) \ge 0\\ \Leftrightarrow \left( {x - 1} \right)\left( {\left( {x - 1} \right)\left( {{x^2} + x + 1} \right) + \left( {x - 1} \right)\left( {x + 2} \right)} \right) \ge 0\\ \Leftrightarrow \left( {x - 1} \right)\left( {x - 1} \right)\left( {{x^2} + x + 1 + x + 2} \right) \ge 0 \\ \Leftrightarrow {\left( {x - 1} \right)^2}\left( {{x^2} + 2x + 3} \right) \ge 0\\ \Leftrightarrow {\left( {x - 1} \right)^2}\left[ {{{\left( {x + 1} \right)}^2} + 1} \right] \ge 0\end{array}\)
(luôn đúng với mọi số thực $x$)
Đẳng thức xảy ra khi và chỉ khi $x = 1.$
Nên A đúng.
+) Đáp án B: Bất đẳng thức tương đương với \({x^4} - {x^2} - 4x + 5 > 0\)
\( \Leftrightarrow {x^4} - 2{x^2} + 1 + {x^2} - 4x + 4 > 0 \)\( \Leftrightarrow {\left( {{x^2} - 1} \right)^2} + {\left( {x - 2} \right)^2} > 0\)
Ta có: \(\left( {{x^2} - 1} \right) \ge 0,\,\,{\left( {x - 2} \right)^2} \ge 0 \)\( \Leftrightarrow \left( {{x^2} - 1} \right) + {\left( {x - 2} \right)^2} \ge 0\)
Dấu bằng xảy ra \( \Leftrightarrow \left\{ \begin{array}{l}{x^2} - 1 = 0\\x - 2 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \pm 1\\x = 2\end{array} \right. \) điều này không xảy ra.
\( \Rightarrow {\left( {{x^2} - 1} \right)^2} + {\left( {x - 2} \right)^2} > 0\) nên B đúng.
Giải phương trình \({\left| {x - 3y} \right|^{2017}} + {\left| {y + 4} \right|^{2018}} = 0\) ta được nghiệm \(\left( {x;y} \right)\). Khi đó \(y - x\) bằng
\({\left| {x - 3y} \right|^{2017}} + {\left| {y + 4} \right|^{2018}} = 0\)
Ta có:
\(\begin{array}{l}\left. \begin{array}{l}\left| {x - 3y} \right| \ge 0\\\left| {y + 4} \right| \ge 0\end{array} \right\} \Rightarrow {\left| {x - 3y} \right|^{2017}} + {\left| {y + 4} \right|^{2018}} \ge 0\\ \Rightarrow {\left| {x - 3y} \right|^{2017}} + {\left| {y + 4} \right|^{2018}} = 0 \Leftrightarrow \left\{ \begin{array}{l}x - 3y = 0\\y + 4 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x - 3.( - 4) = 0\\y = - 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - 12\\y = - 4\end{array} \right.\end{array}\)
Vậy nghiệm của phương trình là $x = - 12$ và $y = - 4.$
Suy ra \(y - x = - 4 - \left( { - 12} \right) = 8.\)

