Trả lời bởi giáo viên
Đáp án đúng: b
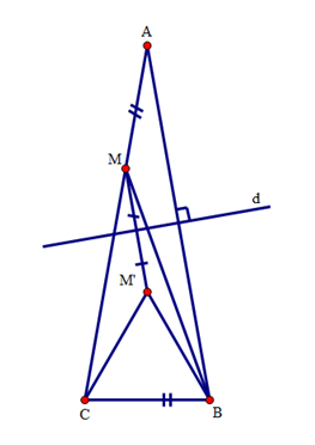
Ta cũng có: \(\widehat {MCB} = {180^0} - \left( {\widehat A + \widehat B} \right) = {180^0} - \left( {{{20}^0} + {{80}^0}} \right) = {80^0}\)
Suy ra \(\widehat {MCM'} = \widehat {MCB} - \widehat {M'CB} = {80^0} - {60^0} = {20^0}\)
Mà \(\widehat {CMM'} = \widehat A = {20^0}\)(góc đồng vị).
Nên \(\widehat {MCM'} = \widehat {CMM'} = {20^ \circ }\)
Suy ra \(M'C = M'M = M'B\).
Ta lại có: \(\widehat {M'MB} = \widehat {M'BM}\) (tam giác \(M'MB\) cân tại đỉnh \(M'\)); \(\widehat {M'MB} = \widehat {MBA}\)(so le trong).
Nên \(\widehat {M'BM} = \widehat {MBA} = \dfrac{1}{2}\widehat {M'BA} = {10^0}\)
Vậy \(\widehat {BMC} = \widehat {CMM'} + \widehat {M'MB} = {20^0} + {10^0} = {30^0}\)
Hướng dẫn giải:
Ta thấy \(\widehat {BMC} = \widehat {CMM'} + \widehat {M'MB}\). Do đó để tính góc \(BMC\) ta lần lượt đi tính góc \(\widehat {CMM'}\) và \(\widehat {M'MB}\).
